インダクタンスの本質：Signal Integrity

[Howard Johnson，EDN]

　今回は、ワイヤーで形成したループのインダクタンスについて論議したい。筆者は、図1に示した4種類のワイヤーループのインダクタンスを計測した。これらのワイヤーは10AWGの単芯絶縁銅線であり、長さは等しい。計測は、各種機器などの金属物体から十分に離れた位置で、各ループの端にプローブを接続してループを垂直に立てた状態で行った。図1のいちばん左のループの直径は25cmであり、インダクタンスの値は4種類の中で最大の730nHであった。右のものほどインダクタンスは小さくなり、右端のワイヤーループでは190nHであった。

図1　インダクタンスの評価用サンプル　各ワイヤーの長さは同じだが、インダクタンスの値は左から順に730、530、330、190nHである。

　このような簡単な実験について言及しようと思ったのは、「この基板のビアのインダクタンスは1nHである」とか「ここで使用しているバイパスコンデンサは500pHのインダクタンスを持つ」などといった表現をしばしば耳にすることがきっかけだった。このような表現を可能にするには、「インダクタンスは信号経路中の各所に独立して存在する」という前提が必要になる。この前提は、回路部品をマクロに扱うのであれば成立する。そして、この前提に立ったものが回路解析におけるキルヒホッフの法則である。この法則によれば、直列に接続した2個のインダクタの全インダクタンスは各インダクタのインダクタンスの和に等しくなるはずだ。

　このキルヒホッフの法則を適用した解析が正しいかどうかは、次に述べる決定的な前提が成り立っているか否かによる。すなわち、「導体間の空間における電磁界は無視できる」といえるかどうかだ。高速デジタル回路に流れる電流は、導体周辺の空間に対し、高速に変化する強い電磁界を形成する。このようなデジタル回路では、キルヒホッフの法則の根本にある前提が成り立たない。言い換えれば、高速回路には、キルヒホッフの法則をそのまま適用することはできないのだ。高速回路では、同法則を補うために、電界に関しては寄生容量について、磁界に関しては寄生インダクタンスについて考慮しなければならない。

図2　電流によって生成される磁界　行きの電流（赤色）によって生成される磁界は、帰りの電流によって生成される、同じ大きさで逆向きの磁界によってほぼ相殺される。

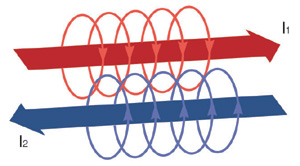
　図2に示したのは、2本の導体の周りに形成される磁界の様子である。これら2本の導体には、図1のヘアピン型のワイヤーの場合と同様に、値が等しく向きが反対の電流が流れている。ここで、I₁が片方の導体から流れ出て、それがヘアピン状に向きを反転し、他方の導体に電流I₂として流れるとしよう。離れた位置から観測すると、I₁によって形成される磁界はI₂によって形成される同じ大きさで逆向きの磁界によってほぼ相殺される。導体の間隔が小さくなればなるほど、この相殺の効果は大きくなり、総和としての磁界エネルギが小さくなる。

　インダクタンスは、このように電流が流れる回路の周りに形成される全磁界エネルギそのものを表現するものである。インダクタンスLと磁界エネルギEの関係を電流Iを用いて表現すると次式になる。

　導体間の距離によって蓄積される磁界エネルギが変化するなら、同様に、その距離によって回路のインダクタンスは変化する。このように磁界が相互作用することが、「回路におけるある部分のインダクタンスは、電流経路全体の位置と形状を規定しない限り決められない」ことの理由だ。インダクタンスは回路の形状により増えたり減ったりし、電流経路のすべての部分がインダクタンスに影響するのである。

　例えば、ビアのインダクタンスは、その付近にある層間接続用のコネクションの位置により変化する。またバイパスコンデンサのインダクタンスは参照面との距離の影響を受ける。インダクタンスは個々の部品の特性を表すのではなく、回路における導体間の空間の特性を表すのである。

＜筆者紹介＞

Howard Johnson

Howard Johnson氏はSignal Consultingの学術博士。Oxford大学などで、デジタルエンジニアを対象にしたテクニカルワークショップを頻繁に開催している。ご意見は次のアドレスまで。www.sigcon.comまたは[e-mail]。