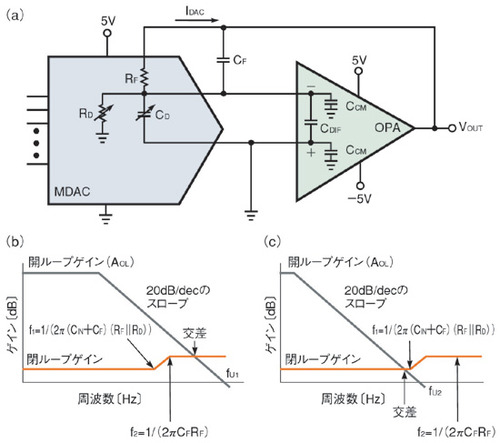
乗算型D-Aコンバータの安定性：Baker's Best

[Bonnie Baker，EDN]

　乗算型D-Aコンバータ（multiplying D-A converter。以下、MDAC）とそのポストアンプは、デジタル領域からアナログ領域への懸け橋となるものだ。MDACは入力のデジタルコードに比例する電流を出力する。この電流出力をポストアンプで電圧に変換することによりアナログ出力が得られる。このような電流‐電圧変換は、アンプと抵抗を利用した一般的かつ簡単な構成で実現できる。しかし、実はその回路は安定性の問題を内包している。

　MDACの出力部は、可変電流源、抵抗、容量を用いて図1（a）のようにモデル化することができる。出力抵抗R_Dと出力容量C_Dの値は、MDACに入力されるコードに依存して変化する。出力抵抗R_Dは、一般的には入力コードを0とした場合は無限大に近似され、フルスケール入力（入力の全ビットが1）とした場合にはフィードバック抵抗R_Fに等しくなる。出力容量C_Dの値も、入力コードの変化に伴い、MDACの出力部から見える内部トランジスタのゲート‐ソース接合の数の違いに対応して変化する。C_Dの値は、フルスケールの入力に対してはデータシートに規定されている。入力コードが0の場合には、フルスケール入力時の約1/2になる。安定性を評価する際には、R_D、C_Dともにフルスケール入力に対応する値を使用すべきである。

図1　MDAC出力のモデル　MDAC出力のモデルは、電流源、抵抗、容量から構成される（a）。（b）は、広帯域アンプ使用時のゲイン特性、（c）は狭帯域アンプ使用時のゲイン特性。

　安定性を決めるもう1つの要素は、オペアンプを用いて構成したフィードバック回路だ。ほとんどのMDACでは、高精度化のためにフィードバック抵抗R_Fがオンチップ化されている。一方、フィードバック容量C_Fには外付け部品が使用される。

　安定性はオペアンプの特性にも依存する。オペアンプにはさまざまな特性指標があるが、安定性に影響する項目はわずかだ。問題になるのは帯域幅f_U、差動入力容量C_DIF、コモンモード入力容量C_CMである。図1（a）の等価回路において、アンプの全入力容量C_INはC_D＋C_DIF＋C_CMで表される。

　系としての安定性は、開ループゲイン特性と閉ループゲイン特性のプロットがどこで交差するかで判断することができる。図1（b）、（c）のように、帯域幅がf₁以下であるか、f₂以上であれば安定だといえる。ここで、f₁は閉ループに対するゼロの周波数であり、f₁＝1/（2π（C_IN＋C_F）（R_D||R_F））となる。一方のf₂は極の周波数であり、f₂＝1/（2πC_FR_F）で表される。

　図1（c）のように、閉ループのゼロの周波数f₁をオペアンプの帯域より高くするには、次の条件を満たすようにC_Fの値を決めればよい。

　図1（b）のように、閉ループの極の周波数f₂より高周波側で開ループゲインのカーブと閉ループゲインのカーブが交差するようにするには、次の条件を満足させる。

　これらのうちいずれかの条件を実現すれば、安定性が容易に確保できる。

　フィードバック容量C_Fの値を決める際には、まずは上記の条件について考える。その上で、浮遊容量、MDACやオペアンプの特性バラツキの影響などに適応するようC_Fの値を調整する。

＜筆者紹介＞

Bonnie Baker

Bonnie Baker氏は「A Baker's Dozen: Real Analog Solutions for Digital Designers」の著書などがある。Baker氏へのご意見は、次のメールアドレスまで。[e-mail]