SAR型A-Dコンバータの入力バッファ回路:アンプ回路定数の決定法を学ぶ(2/2 ページ)
SAR型A-Dコンバータの性能を引き出すには、アナログ信号入力部に、オペアンプを使用した適切なバッファ回路を配置する必要がある。この入力バッファ回路は単純な構成のものでもかまわないのだが、その定数設計は意外に複雑な作業となる。そこで本稿では、最も単純な構成の入力バッファ回路を例に、定数決定手法の詳細を解説する。
製造ばらつきの考慮
RINとCINの値を決定するためには、オペアンプについて、もう1つ知っておくべきことがある。それは製造ばらつきの存在である。
オペアンプの性能は、内部素子の製造ばらつきによって誤差を持つ。まず、オペアンプの構成要素であるコンデンサの値には、最大±15%の誤差が生じる。また、オペアンプを構成するトランジスタのトランスコンダクタンスは±5〜±15%ほど変動する。こうしたことを踏まえ、3σ(標準偏差の3倍)を考慮した25℃におけるユニティゲイン周波数fUの値は、±20%の範囲でばらつくと考えるとよいだろう。
製造ばらつきによる誤差を考慮に入れて安定性を確保するためには、fCL=fU/2、fZ=fCL/2(=fU/4)の関係を目標にするとよい。あるいはGZが6dBになるようにすることを目標とすると言い換えてもよいだろう。GZを6dBとすると、0dB=6dB−20log(fCL/fZ)、つまりfCL=2×fZ(すなわち、fZ=fCL/2)となる。仮にGZが3dBだとすると、式(5)から0dB=3dB−20log(fCL/fZ)、つまりfCL=1.41×fZ(すなわち、fZ=fCL/1.41)となる。このようにゲインと周波数の関係を調整することで、RINとCINの最適値を決定することができる。
基礎理論の検証
ここまでに述べた内容について、実験を通して検証を行ってみよう。
■入力バッファ回路のみの検証
検証には、入力バッファ回路の具体例を2種類用いる。使用したオペアンプ(Texas Istruments社の「OPA364」)のユニティゲイン周波数fUは6.45MHz(データシート上の標準値は7MHz)、開ループ出力抵抗ROは110Ωである。両入力バッファ回路では、いずれもCINとして1500pFのコンデンサを使用することにしよう。また、両入力バッファ回路でターゲットとするクロスオーバー周波数fCLはfU/2(3.23MHz)で、RIN、CINを付加した状態でのゼロの周波数fZとしてはfU/4(1.61MHz)を目標とする。
2つの回路は、RINの値だけ異なるものにする。それにより、比較的安定している回路Aとかろうじて安定している回路Bを構成し、SARコンバータを接続しない状態、接続した状態の2条件で評価を行う。ここで、比較的安定しているというのは、ボード線図が図3のようになるケースで、かろうじて安定しているというのは、ボード線図が図4のようになるケースである。回路A、回路Bに対してステップ信号を入力し、図1のVIN(SARコンバータの入力部)における応答に現われる影響を観測する。オペアンプは図1のとおり、閉ループゲインが1V/Vのバッファ構成とする。
比較的安定している回路AのRINの値は66.5Ωとした。このCIN、RIN、ROの組み合わせにより、ポールの周波数fPは式(1)から601kHz、開ループゲインGPは式(3)から20.6dBとなる。また、ゼロの周波数fZは式(2)から1.596MHz、開ループゲインGZは式(4)から3.63dBと求まる。
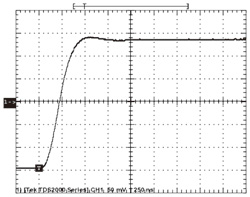
図5に示したのは、オペアンプの非反転入力端子に振幅280mVppのステップ信号を入力した場合のVINにおける応答波形である。VINにおける信号は、1μsの間安定している。この特性は、(設計仕様にもよるが)SARコンバータを用いる場合の結果として望ましいものだと言える。
一方、かろうじて安定している回路BのRINの値は15Ωとした。RIN、CIN、ROの値から、ポールの周波数fPは849kHz、開ループゲインGPは17.6dBとなる。ゼロの周波数fZは7.074MHz、開ループゲインGZは〜19.23dBと求まる。
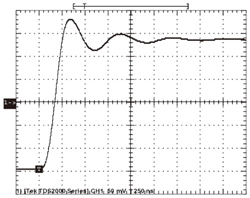
図6は、図5と同じ条件で回路Bに信号を入力した場合の応答波形である。かろうじて安定しているこの回路Bでは、応答波形に、リンギングを伴うオーバーシュートが生じている。これはSARコンバータの入力としては望ましくない結果だ。この信号を基にSARコンバータが生成する出力は、不正確なものとなる。
■SARコンバータを用いた検証
上の結果は、SARコンバータを接続していない状態でのものである。SARコンバータを接続すると負荷が変化するものの、同様の結果が得られる。ただし、SARコンバータのサンプリングスイッチが閉じる際には、キックバック電流が生じる。そのため、オシロスコープによって12ビット精度の変化を観測することは難しい。そこでもう1つの測定手法を適用する。なお、SARコンバータとしてはTexas Instruments社の「ADS7886」を用いる。
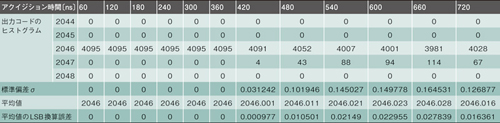
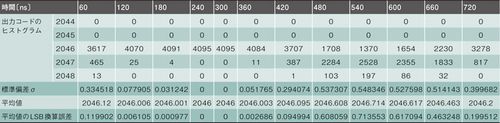
まず、入力バッファ回路とSARコンバータを図1のように接続する。その上で、オペアンプの非反転入力端子に一定の電圧を印加する。SARコンバータのアクイジション時間を60nsとし、出力コードの測定を4095回繰り返し行う。その後、アクイジション時間を60nsずつ増加させながら4095回ずつ測定を継続する。この測定を、回路A、回路Bを用いた場合のそれぞれに対して実施した。
回路A、回路Bに対する計測結果をそれぞれ表2と表3に示す。「出力コードのヒストグラム」の項は、出力コードとして得られた2046〜2048という値が、4095回の測定のうち、何回観測されたかを表している。表2、表3のデータから、比較的安定した回路Aを用いた場合には、標準偏差が小さく平均値がより一定になることがわかる。かろうじて安定している回路Bの平均値には0.7LSB以上の誤差があるが、比較的安定した回路Aの誤差は0.03LSB未満に抑えられている。
設計手順のまとめ
ここまでに説明した基礎知識を踏まえて、最後に、RINとCINの値を決定する手順をまとめておく。
まず、SARコンバータを使用する場合には、入力バッファ回路用に適切なオペアンプを選択することが非常に重要である。オペアンプのノイズ、帯域幅、セトリング時間などについて、SARコンバータのS/N比、SFDR(Spurious Free Dynamic Range)、入力インピーダンス、サンプリング時間などと突き合わせて検討しなければならない。加えて、本稿で説明したとおり、CINの値に影響を与えるサンプル‐ホールドコンデンサCSHの値に注意しなければならない。
CINの値を決定する際には、以下の条件を満たすようにするとよい。
この値が決まれば、アクイジション時間定数Kの値を算出することができる。SARコンバータの分解能(ビット数)をNとすると、定数Kは以下の式で求められる。
設計要件とSARコンバータの性能により、SARコンバータのアクイジション時間が決まる。そこで、アクイジション時間tACQを用いて、ローパスフィルタを付加した場合のゼロの周波数fZを算出する(以下参照)。
これらの値が決まったら、以下の式により、回路の安定性を検証する。
ゼロの周波数fZとCINから、以下の2つの式によってRINの値が決定できる。
以上でCINとRINの値が決まるが、最後に、安定性を確認するために、ローパスフィルタを付加した場合のポールの周波数fPを以下のように算出する。
続いて、ローパスフィルタを追加した場合の開ループゲイン特性において、ゼロのゲインGZを調べる。回路を安定させるためには、この値は6dB以上でなければならない(以下参照)。
この式が成り立つことが確認できれば、設計作業は完了である。設計が完了したら、安定性を検証するために実際に回路を構成して評価を実施することが重要である。
Copyright © ITmedia, Inc. All Rights Reserved.