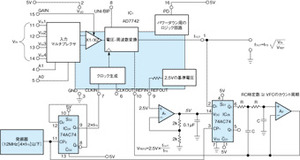
図1に示したのが、この方式を実現する回路である。VFC(IC1)としてはAD7742を用い、外部回路によって上述した方式を実現している。
出力周波数に常に比例する基準電圧VREF2は、オペアンプA1、フリップフロップIC2B、およびオペアンプA2によって得ている。オペアンプA1によりAD7742が内蔵する基準電圧2.5Vを増幅し、その出力がフリップフロップIC2Bの電源となり、IC2BとオペアンプA2とによって、出力周波数に比例する基準電圧VREF2を生成する仕組みだ。この基準電圧VREF2 の精度は、VFCに入力するクロック波形のデューティ比が正確に50%であるかどうかに依存する。この条件は、フリップフロップIC2Aの1/2分周動作によって実現する。
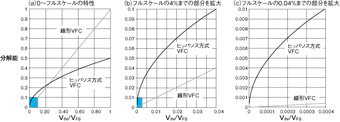
この回路により、フルスケールに対してレベルの小さい信号に対する分解能が飛躍的に改善する(図2)。例えば、VIN/VFSが0.0004(1mV/2.5V)の場合、図2(c)に示すように、線形VFCでは分解能も0.0004になり2500カウント(1/0.0004)を要する。つまり、最大フルスケール周波数が3MHzならば、カウント周期として833μsが必要だ。それに対し、ヒッパソス方式では分解能が0.01になり、100カウント(1/0.01)、つまり33μsのカウント周期で済むので、25倍の改善効果が得られる。ヒッパソス方式の非線形VFCからの出力は、ソフトウエアを利用すれば容易に線形出力に変換できる。
紀元前500年ごろ、ギリシアに「メタポンタムのヒッパソス(Hippasus of Metapontum)」と呼ばれる哲学者がいた。彼はピタゴラスの弟子で、平方根の持つ興味深い特質を見出したことで知られている。本稿では、そのような平方根の特質を利用した非線形方式の電圧−周波数コンバータ(VFC:Voltage to Frequency Converter)を紹介する。その方式を用いれば、VFCの小信号に対する分解能を数桁も広げることができる。
一般的な線形VFCは、最も古いタイプのA-Dコンバータとして使われていた。構成が簡単であり、ノイズ除去性能が良好であるといった特徴を備えることから、現在でもなお広く利用されている。しかし、線形VFCを用いたA-D変換では、ダイナミックレンジと変換時間との間に直接的な比例関係があることが致命的な欠点となる。線形VFCの電圧分解能VRESは、フルスケールに対応する基準電圧VREF、フルスケールに対応する周波数fFS、変換出力パルスの数をカウントする周期Tを用いて以下のように表される。
VRES=VREF/(fFS×T)
従って、入力ダイナミックレンジを広げる、言い換えれば高い分解能を得るには、カウント周期を長くする必要がある。そのため、フルスケール周波数の高い高価なVFCを使ったとしても、変換速度が遅くなることは避けられない。具体的な例として、米Analog Devices社のVFC「AD7742」をA-Dコンバータとして使用し、1mVの分解能を得るケースを考える。AD7742の最大フルスケール周波数fFSは3MHz、フルスケール基準電圧VREFは2.5Vなので、最小のカウント周期Tは、2.5V/1mV/3MHz=833μsとなる。このカウント周期の値は、変換速度が1200サンプル/秒であるということを意味するので、多くの用途では遅すぎて使えないという結論になるだろう。
本稿で紹介する“ヒッパソス方式”の非線形VFCは、線形関数ではなく、半放物線関数を変換式として用いる。それによって、上述した問題点を解決する。この方式では、基準電圧として、線形VFCで使われる固定の基準電圧VREFではなく、出力周波数fOUTに比例する電圧VREF2を使用する。このVREF2は、以下の式で表される。
VREF2=VREF×fOUT/fFS
これにより、出力周波数fOUTについては、入力電圧VINとの間に次のような関係が成り立つ。
fOUT=VIN×fFS/VREF2=VIN×fFS/(VREF×fOUT/fFS)
この式を変形すると、以下のようになる。
(fOUT/fFS)2=VIN/VREF
さらに変形すると以下のようにまとめられる。
fOUT=fFS×(VIN/VREF)1/2
Copyright © ITmedia, Inc. All Rights Reserved.