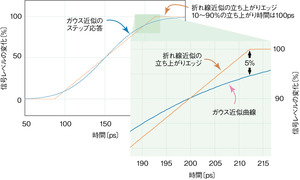
読者が普段扱っているデジタル信号を近似する場合、図1に示す2つの手法のうち、いずれが適切だろうか。折れ線近似とガウス近似の2つである。折れ線近似では、信号が急激に上昇し始め、続いて完全な直線状の傾斜で上昇し、最後は上限にぶつかって終わっている。このような動きは現実の信号では起こらない。一方の滑らかな曲線は、ガウス近似を適用したものである。この曲線は釣鐘型のガウス曲線を時間積分することで得られる。ガウス近似では、始端も終端も滑らかであり、中央部は高速かつ単調な増加となる。このほうがデジタル信号らしく見えるが、それには当然の理由がある。
線形システムの解析の分野に中心極限定理(Central Limit Theorem)を適用すれば次のようなことが言える。すなわち、同等の帯域制限特性を持った多数の要素から成るシステムでは、ステップ応答は、要素数が無限に近づけばガウス分布になるということである。この定理は高速デジタル信号を扱うシステムにも当てはまる。その種のシステムのドライバ回路は、同等の動作特性を持つ多数の回路要素が直列に多段接続された構成となっているからである。
多段構成のI/Oドライバであれば、シリコン素子からのnAレベルの電流を数mAの電流に高速変換し、プリント基板パターンに送出することができる。このような動作は、単一のFETで構成したアンプでは不可能だ。仮に単一のFETのゲートサイズを十分に大きくし、プリント基板上で扱うレベルの電流を流せるようにしたとしても、そのゲートの高速な充電には、シリコン素子内部で流し得るレベルの電流では不足する。回路を多段に分割し、直列に接続する手法のほうがより優れている。その場合、各段のゲートサイズは、その前段に比較して指数関数的に大きくする。この種の回路の設計者たちは、最大の性能を得るために、多大な時間をかけて各ドライバの段数や各段の構成を慎重に設計しているのだ。
そして、この点に中心極限定理が働く理由がある。例えば、10段構成のI/Oドライバを設計するとしよう。DC動作であれば、回路は理想的に働く。しかし、動作周波数を上げるとさまざまな寄生効果の影響が出始め、帯域が制限されていく。各段には20種類程度の寄生効果が考えられるはずなので、完全な設計を行うためには、10段構成全体としては200個ほどの効果に対処しなければならないことになる。
システム全体としての帯域は、ほかにどれほど優れた素子が存在するとしても、全体の中で最悪な動作の素子によって決定される。全体の動作を向上させるには、最悪な部分を改善することから取り組むべきだ。最悪な性能の要素を順に見出し、一度に1つずつ改善し、それ以上は有意な性能改善が難しくなるレベルまで進める。それにより、すべてのシステム要素が均一な限界性能に達したら、システムの改善が完了し、製品として製造するにふさわしい状態になる。こうした過程を経て作られたシステムは、同等に性能を制限する要素が多数直列接続されたものとなる。先述した理由から、このシステムのステップ応答はガウス曲線に近い形状になる。
図1に示すように、時間領域では、ガウス近似と折れ線近似との差異は最大5%に過ぎない。この程度の差異なら重大なことではなさそうにも思える。しかし、周波数領域で評価すると、この折れ線近似に見られる鋭角の折れ曲がりにより20dBに達する差異が生じ、重大な誤差要因となる。
<筆者紹介>
Howard Johnson
Howard Johnson氏はSignal Consultingの学術博士。Oxford大学などで、デジタルエンジニアを対象にしたテクニカルワークショップを頻繁に開催している。ご意見は次のアドレスまで。www.sigcon.comまたはhowie03@sigcon.com。
Copyright © ITmedia, Inc. All Rights Reserved.