フーリエ理論では、完全な方形波は、無限個の正弦波の和として表現される。このとき、各正弦波には、方形波の基本周波数に対する偶数次の高調波は含まれず、すべて奇数次の高調波となる。それぞれの正弦波の振幅は、順に1、1/3、1/5、1/7、……といったパターンの値になる。
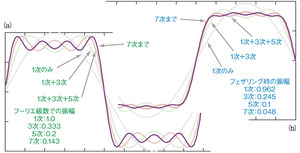
図1(a)は、方形波の高調波級数のうち、最初の数項を順次足していったものである。1次のみの波形は、方形波の基本周波数に対応する単純な正弦波となる。そして、その基本周波数の正弦波に3次高調波を加え、さらに5次高調波を加えという具合に、高次の高調波を加えていくことで、波形はだんだんと角ばってくる。しかし、図のとおり、波打っている部分も見て取れる。
多くの技術者は、「方形波を適切に表現するには、何次までの高調波を使用すべきなのか」という疑問を抱くであろう。これは、「デジタル伝送システムには、どの程度の帯域が必要なのか」という疑問に置き換えることもできる。
この問題について考えるために、まずは各高調波の振幅について検討してみる。上述したように、フーリエ理論では無限個の和という概念が使われているが、これは実際には実現不可能なものだ。そこで、有限個の正弦波の和で波形を表現するために、理想的な無限級数和とは異なる振幅分布を用いる。図1(b)では、7次から先の無限個の高調波の振幅を単純にすべて0にするのではなく、高調波列のうちの最終項(この例では7次)の振幅が十分に小さくなるよう順次滑らかに減少(フェザリング)させている。その結果、最終項の部分で生じる不連続な変化の影響が緩和され、よりきれいな波形が得られている。
出力波形の品質には、使用する高調波の数と、各次数の正弦波に対する振幅分布の妥当性が影響を及ぼす。デジタル伝送システムで言えば、所要の帯域幅について考える際には、−3dB減衰する周波数だけではなく、伝達関数全体の詳細な形状が結果に影響を及ぼすということだ。Harry Nyquist氏は、そうした概念をデータ伝送に関する定理として具体化した。その定理からは、信頼性のあるデジタル通信を実現するためには、レシーバが無限の複雑さを持ち、システムの伝達関数が全体にわたって完全に制御可能であるという条件の下、その(レシーバの)帯域幅は、システムのデータレートの半分以上でなければならないという結論が得られる。
あるシステムがデータ転送周波数Bでデータを送出すると仮定する。送出可能な最高速の変化パターンは1、0、1、0、……となる。つまり、長さ2ビットの単位での繰り返しとなるので、このパターンの基本周波数はBの半分に等しい。Nyquist氏によれば、その信号の相当の部分を受信すれば、すべてのデータを復元できるということになる。
しかし、無限の複雑さを持ち、システムの伝達関数の全体を完全に制御可能なレシーバなど存在しない。そのため、セットアップ‐ホールド条件に対して十分なマージンを持ち、アイパターンが良好なデジタルシステムを得るには、単にデータ転送周波数に対してだけでなく、立ち上がり時間/降下時間についても十分に考慮しなければならない。
筆者の考えは、「立ち上がり/降下時間Tがシステムを伝搬する過程で保持されるために必要な帯域幅は、ほぼ(1/2)/Tに等しい」というものだ。立ち上がり/降下時間をデータ転送周期の10%とすると、Tは0.1/Bである。これを基に少し計算を行うと、システムに必要な帯域幅は0.5/T、すなわちB の5倍ということになる。このことから、多くの技術者が抱く「何次までの高調波が必要なのか?」という疑問に対する筆者の答えは、「5次までを使う」となる。
<筆者紹介>
Howard Johnson
Howard Johnson氏はSignal Consultingの学術博士。Oxford大学などで、デジタルエンジニアを対象にしたテクニカルワークショップを頻繁に開催している。ご意見は次のアドレスまで。www.sigcon.comまたはhowie03@sigcon.com。
Copyright © ITmedia, Inc. All Rights Reserved.