進化したオシロスコープを使いこなせる、 真のエンジニアになろう:いまさら聞けないオシロスコープ入門(1)(2/3 ページ)
電子機器や組み込み機器などの開発において欠かすことのできないオシロスコープについて、その操作方法や概念をあらためて解説します。
誤差を小さくするには
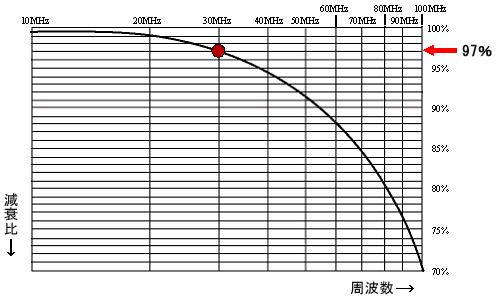
それでも約30%もの大きな誤差となります。もっと小さな誤差で済ませるには、もっと広い周波数帯域を持つオシロスコープを使います。約1GHzくらいまでのオシロスコープの高域減衰特性はガウス曲線に近似していますので、この曲線をなぞると、もっと誤差の小さな結果を得るための周波数帯域を推測することができます。
100MHzのオシロスコープの例で見ると、30MHzくらいまでの周波数の測定に止めれば、約3%の誤差で測定できることになります。これを「3倍」の法則といいます。言い換えると、3%の誤差にするには3倍広帯域のオシロスコープを使用すればよいことが分かります。
パルス波形の形はどう見える?
問題です。「最高周波数帯域20MHzをうたうオシロスコープで繰り返し周波数10MHzのパルス波を観測すると?」
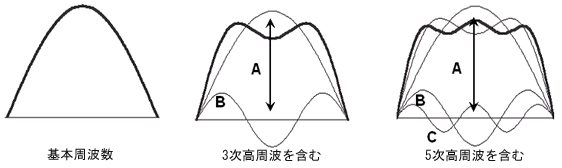
答えは「波形は丸まった台形波に見える」です。パルス波の形状は、3次5次7次……と無数の奇数高次の高調波を含むことにより、形成されています。
ところが、高次の50MHz(5次)、70MHz(7次)、……は周波数帯域20MHzのオシロスコープでは減衰が激しく、パルス形状の形成が再現できません。結果、オシロスコープが表示する波形は、パルス波にはとても見えません。せいぜい3次高調波(30MHz)がわずかに通過し、波形を辛うじて台形にとどめるのが精いっぱいです。
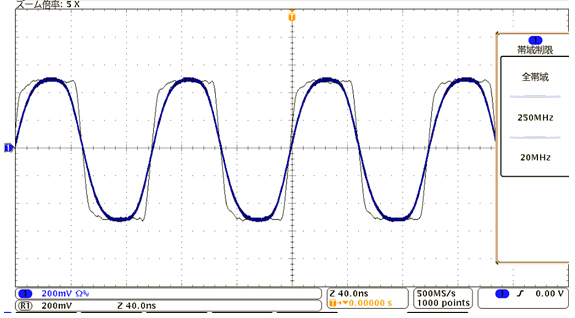
図4では、250MHzのオシロスコープで取り込んだ波形を細い黒色で、20MHz帯域制限機能により、20MHzのオシロスコープとして取り込んだ波形は太い青色で表現されています。青色の波形は立ち上がり/立ち下がり部が斜めに表現され角も丸まっています。
パルスの繰返し周波数と周波数帯域の関係
問題です。パルス波形を正確に再現するために必要なオシロスコープの周波数帯域とパルスの繰り返し周波数との間には一定の法則がある/何の法則もない?
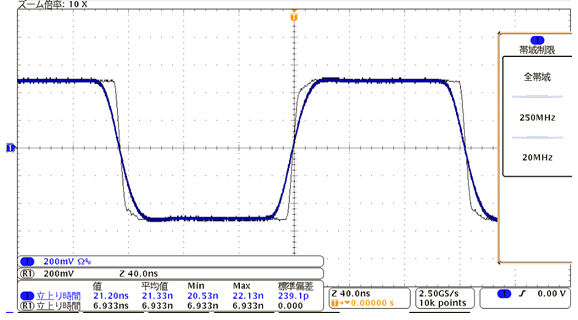
答えは「何の法則もない」です。パルス波は、その繰り返し周波数が5倍ほどの波数帯域のオシロスコープで見ればイイと聞いたことがあるかもしれません。5倍の高調波が再現できれば、なんとかパルス波に見えるということからきた経験則です。実際に4MHzのパルス波を20MHzと250MHzのオシロスコープで見たのが図5です。5倍である20MHzの周波数帯域を持つオシロスコープ(太い青色)では立ち上がり/立ち下がり部分も鈍ります。
測定した立ち上がり時間も大きな誤差を持ちます。よって、「繰り返し周波数の5倍」ではダメなことが分かります。細い黒色の波形は、パルス波の立ち上がり時間に対して「4倍」以上の高速立ち上がりを持つオシロスコープで見た波形です。立ち上がり部の急峻な変化が正確に表現されていることが分かります。法則は、「周波数とは何のかかわりもなく、立ち上がりの4倍」です。4倍の根拠は次ページの説明を見てください。
Copyright © ITmedia, Inc. All Rights Reserved.