DSPはFPGAで作れる？：イチから学ぶDSP基礎の基礎（5）（3/3 ページ）

今回は、DSPとFPGAを比較してみたいと思います。この比較は、言いかえれば、“デジタル信号処理にはソフトウェア処理とハードウェア処理のどちらが向いているか”ということになります。

[日本テキサス・インスツルメンツ]

　実際に製品を設計するに当たっては、デバイスの性能以外にチップの値段の差も考慮する必要があります。大規模なFPGAを使えばDSPをしのぐ演算能力を有数する回路を実現可能ですが、そのようなFPGAは値段もDSPよりはるかに高価となります。また、DSPでもFPGAでも無理なく実現可能であっても、コストの面でDSPの方が有利となるアプリケーションも多いのです。

　最後になりますが、サンプリング周波数と処理の内容に応じて1つのシステムの中でDSPとFPGAを使い分けた例のブロックダイヤグラムを図6に示します（現実の製品のブロックダイヤグラムではありません）。一部の処理をデジタル化した受信機ではこのようにDSPを用いた復調およびデータ伸張処理等の前段の処理（中間周波段のフィルタリングなど）にFPGAを用いることがよくあります。

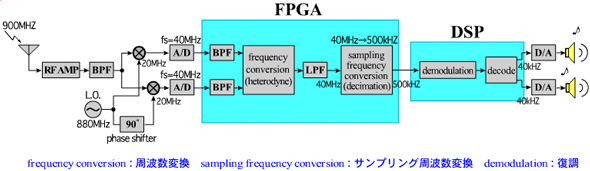
図6 1つのシステムの中でDSPとFPGAを使い分けた例（デジタル受信機）　中間周波フィルタの処理（サンプリング周波数20MHz）をFPGAで行い、サンプリング周波数を500kHzに落とした後、DSPで復調・伸張処理を行っている

帯域制限信号のサンプリング定理

　いままでの説明でサンプリング周波数に応じてDSPとFPGAを使い分ければ、あるいは両者を組み合わせれば、うまくデジタル信号処理システムを構成することができる例があることが分かりました。一例として上げた図6では、周波数900MHzの信号をアナログ処理で20MHzに変換し、サンプリング周波数40MHzでA/D変換してからFPGAでの処理を行い、サンプリング周波数変換（sampling frequency conversion）後の処理をDSPで行っています。

　ここで次のような疑問をお持ちの方はいないでしょうか？

疑問：FPGAでサンプリング周波数変換処理をしてサンプリング周波数を40MHzから500kHzに落としているのはサンプリング定理に違反しているのではないか？周波数20MHzの信号をサンプリング周波数500kHzで処理することはできないはずではないか？

　実は、図6に示したような変調信号を扱った場合は、きちんとサンプリング定理を満たしているのです。以下、順を追って説明しましょう。

　・サンプリング定理（α）

　 入力信号の最高周波数の2倍以上のサンプリング周波数でA/D変換すれば元の信号の情報を失わずにアナログ信号を離散化（デジタル化）できる。

　上記（α）のようにサンプリング定理を覚えている方が多いと思いますが、少し違った表現をするとサンプリング定理は次のようになります。

　・サンプリング定理（β）

　 入力信号帯域幅の2倍以上のサンプリング周波数があれば、元のアナログ信号の情報を失わずに離散時間処理（デジタル処理）ができる。また、直流（0Hz）から周波数成分を持つ信号を扱う場合、2つの定理により定まるサンプリング周波数は同じになる。しかし帯域制限信号を処理する場合、必要とされるサンプリング周波数は（α）ではなく（β）の定理によって定まるサンプリング周波数で必要十分となる。

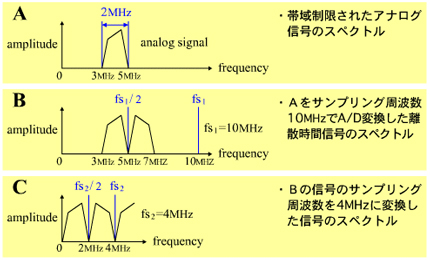
　具体例として図7Aのような帯域制限信号（帯域幅2MHz）をA/D変換してデジタル処理することを考えてみます。帯域制限信号はLPFやBPFによって信号の帯域幅が有限化された信号ですが、ここでは図Aに示すようにBPFによって上下両端の周波数が制限された信号を取り上げます。一般の無線通信に用いられる変調処理を施した信号はこのような有限の帯域幅を持つ信号となります。

　図7Aの信号をデジタル処理する場合、最高周波数は5MHzなので、単純に考えればサンプリング周波数10MHz以上でA/D変換して、所望のデジタル処理を行った後10MHzでD/A変換すればよいことになります。

図7 信号のスペクトル図

　サンプリング周波数10MHzでA/D変換した信号のスペクトルは、図7Bのようになります。しかし（β）のサンプリング定理に従えば、実はサンプリング周波数は帯域幅（2MHz）の2倍の4MHzでこの信号の処理を行うことができます。つまり図9（途中でサンプリング周波数を4MHzに落としての処理フロー）に示すように、途中でサンプリング周波数変換処理を施せば、低いサンプリング周波数で所望の処理を行い、単位時間内の演算量を低減することができます。

　ただし、A/D・D/Aのサンプリング周波数はあくまでも（α）のサンプリング定理に従った10MHzであることに注意してください。なおサンプリング周波数10MHzでA/D変換した信号図7Bを、サンプリング周波数4MHzに変換した信号のスペクトルは図7Cのようになります。

　図7Bの3M〜5MHzの周波数成分が、図7Cでは0M〜2MHzにシフトしていますが、帯域幅2MHzの信号成分は失われていません。よってサンプリング周波数4MHzで何ら問題なく各種の処理を行い、その後にまたサンプリング周波数を10MHzに変換すれば、ずっとサンプリング周波数10MHzで処理したのと同じ結果を得ることができます。

　このように帯域制限信号を取り扱うのであれば、（β）のサンプリング定理に基づいて必要最低限のサンプリング周波数でデジタル処理を行うことが可能です。つまり信号の最高周波数、あるいは中心周波数だけを見たのではDSPでは処理が不可能であるかのように見えても、帯域制限された信号であるためにDSPで十分処理可能な場合があるのです。

サンプリング周波数変換処理はDSPでもFPGAでも可能

図8 サンプリング周波数10MHzでの処理フロー

図9 途中でサンプリング周波数を4MHzに落としての処理フロー　サンプリング周波数10MHzではなく、4MHzで処理可能なので、その分、単位時間内の演算量を削減できる。サンプリング周波数変換処理には効率的な実現方法があるので、オーバヘッドは小さくて済む

　サンプリング周波数の変換処理は、DSPでもFPGAでも可能です。DSPでソフト的に処理する場合、図を比較すると本来の所望の処理に対してサンプリング周波数変換のための余分な演算が付け加わることになりますが、周波数変換には効率的な実現手法があるため、通常はサンプリング周波数低減による演算量削減効果の方が勝ります。

　一方、変換前後のどちらかのサンプリング周波数が非常に高くソフトウェアでは処理が難しい場合には、ハードウェア、すなわちFPGAや専用のLSIでサンプリング周波数変換を行います。

---

　次回は番外編として、サンプリング周波数変換でできる効率的なFFT分析について解説します。