デジタル変換時の波形を うまく見るためのポイント：いまさら聞けないオシロスコープ入門（2）（1/2 ページ）

デジタル・オシロスコープの動作は、まず波形をデジタイズして、デジタル点を得ることから始まります。今回は、デジタル変換時の波形をうまく見るためのノウハウをご紹介します。

[稲垣 正一郎，日本テクトロニクス]

＠IT MONOistで掲載された記事を転載しています

サンプル・レートが波形を変える（デジタル･オシロスコープ独自の注意）

　デジタル・オシロスコープの動作は、まず波形をデジタイズして、デジタル点を得ることから始まります。

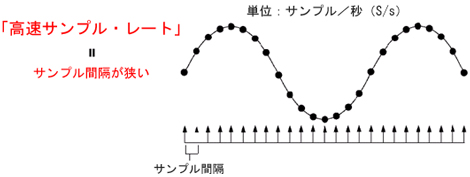
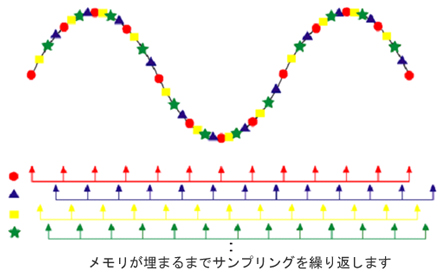
　波形を一定間隔でデジタイズする過程をサンプリングと呼び、サンプリングするスピードをサンプル・レート（単位はS/s：サンプル・パー・セック）と呼びます。デジタル・オシロスコープにとって、波形を正しく再現できるかどうかは、前回の周波数帯域や立ち上がり時間に加え、サンプル･レートによっても大きく左右されます。

図1 1秒間に何回サンプリングするかという性能

サンプル･レートでサイン波が変形

　ここで問題です。観測したい波形の繰り返し周波数より……

• サンプル・レートが低いと、単発取り込みにおいて致命的な問題を起こす
• サンプル・レートが低くても、単発取り込みにおいて致命的な問題を起こさない

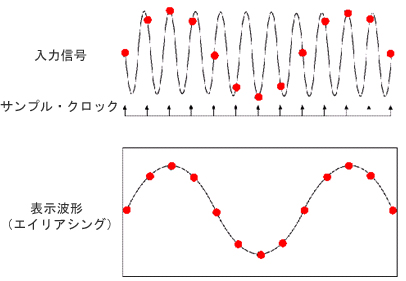
　答えは「サンプル・レートが低いと、単発取り込みにおいて致命的な問題を起こす」です。サンプリング対象の波形の繰り返し周波数に対して、サンプル･レートが高く（速く）なくてはなりません（ナイキストの定理によると、2倍より高速のサンプリングが必要です）。この条件がかなえられなければ、エイリアシングと呼ばれる現象が起きる場合があり、その波形はまったく正しくありません。オシロスコープがあり得ない波形を作ってしまうのです。

図2 DSOを使用したとき、信号周波数とサンプル・レートの関係により表示される「偽り」の波形

　エイリアシングの例を出すまでもなく、オシロスコープが波形を点で表すことを考えれば、サンプル点は多いほど波形を忠実に再現できることが容易に想像できると思います。サイン波の周期より5倍から10倍速いサンプル・レートがあれば、サイン波の再現において良い結果を生みます。つまり100MHzのサイン波を観測するには、最高サンプル･レート500MS/sから1GS/sのサンプル・レートを持つオシロスコープが好ましいことになります。

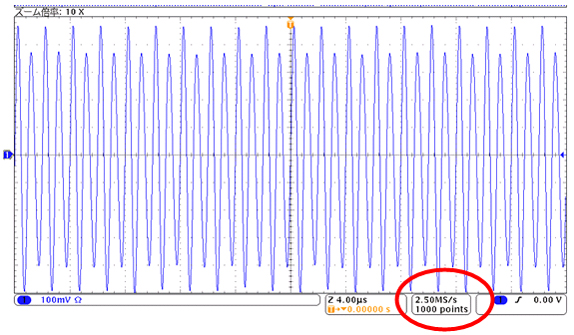
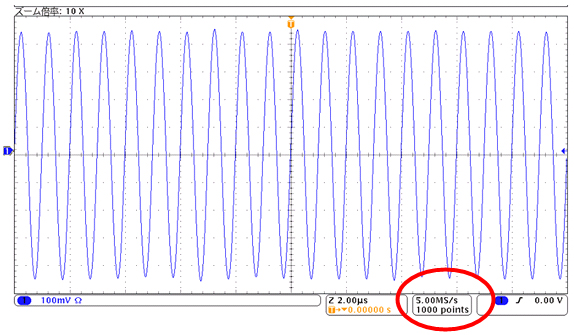
　図3、4はサンプル・レートが2.5倍のときと5倍のときの例です。2.5倍のときは一定振幅であるはずのサイン波がオシロスコープの画面においては変動して見えます。理論では2倍以上のサンプル・レートがあり、非常に多くの周期が取り込めれば、サイン波が正確に再現できることになりますが、実際にはオシロスコープのメモリに取り込まれたサイン波の数も有限です。これは、5倍から10倍速いサンプル・レートの必要性が実感できる波形です。

図3 一定振幅の1MHzのサイン波を、サンプル・レート2.5MS/sでとらえた波形

図4 一定振幅の1MHzのサイン波を、サンプル・レート5MS/sでとらえた波形

特殊な手法

　さて、問題です。観測したい波形の繰り返し周波数より……

• サンプル・レートが低いと、いかなる場合も救いようがない
• サンプル・レートが低くても、繰り返し波形ならば、救える場合がある

　答えは「サンプル・レートが低くても、繰り返し波形ならば、救える場合がある」です。オシロスコープの中にはサンプル・レートが5倍どころか、逆に周波数帯域より低いオシロスコープもあります。周波数帯域より遅いサンプル・レートでは波形の再現はできないと思えるかもしれませんが、これはキーデバイス（A/Dコンバータ）の性能不足を特殊な取り込み手法でカバーしたオシロスコープです。

等価時間サンプルについて

　等価時間サンプルはサンプリングのスタート点を少しずつずらして繰り返しサンプリングすることにより、結果的に多くのサンプル点を波形上に打つ手法です。ただし、この手法には大きな制限があり、再現できる波形は、同じ形を繰り返す、繰り返し波形でなくてはなりません。測定の対象が繰り返し波形ではないとき、この手法は使えませんので、サイン波の周期より5倍から10倍速いサンプル・レートを持つオシロスコープに越したことはありません。

図5 等価時間サンプリング（Equivalent Time Sampling）　数回の取り込みでデータ・ポイントを取る方法（繰り返し信号のみ使用可能）

パルス波での法則

　問題です。パルス波の再現において、パルスの繰り返し周波数と最適なサンプル・レートには、

• 一定の関係がある
• まったく関係がない

　答えは「まったく関係がない」です。パルス波の再現においては、サイン波よりもっと注意が必要です。立ち上がり時間のお話で説明したように、パルス波の繰り返し周期（周波数）はまったく考慮する必要がありません。一番高い周波数成分を持つ急峻（きゅうしゅん）な変化部分を考慮しなくてはなりません。この急峻な部分を正確に再現しようとすれば、そこに十分な数のサンプル点を打てることが大事です。

　一般的に立ち上がり部分は4〜5個のサンプル点が打てれば再現が可能だといわれます。そこで、急峻な部分の立ち上がり時間を知れば、そこに4から5個以上のサンプル点を打つのに必要なサンプル・レートが計算できます。例えば、40nsの立ち上がり時間を持つ信号の再現においては、10nsから8nsの間隔でサンプルを打てば4〜5個のサンプル点が得られます。ちなみに、サンプル間隔10nsをサンプル・レートに換算すると100MS/sとなります。