サンプリング周波数変換でできる 効率的なFFT分析：イチから学ぶDSP基礎の基礎（6）（4/4 ページ）

今回は、DSP入門とは少し離れて、サンプリング周波数変換について解説します。サンプリング周波数変換技術を用いてFFT分析を行うためのヒントについても触れています。

[日本テキサス・インスツルメンツ]

任意の周波数比のサンプリング周波数変換

　インターポレーションとデシメーションを組み合わせれば、任意の周波数比のサンプリング周波数変換ができます（ただし有理数比となります）。周波数比M:Lのサンプリング周波数変換システムのブロック・ダイヤグラムは図17aのようになり、これはサンプリング周波数アップのシステムとサンプリング周波数ダウンのシステムを縦属接続しただけです。

　LPFが2つありますが、これを1つにまとめて一般化したサンプリング周波数変換システムのブロック・ダイヤグラムは図17bとなります。

　例えば、サンプリング周波数32kHzのMDと48kHzのDAT（Digital Audio Taperecorder）の間のサンプリング周波数の変換は図17cおよび図17dの回路で可能です。MD→DAT変換の場合（図17c）もDAT→MDの変換の場合（図17d）もエリアジングひずみ発生を避けるためのLPFフィルタのカットオフ周波数は同一であることに気を付けてください。LPFのカットオフ周波数は入出力の低い方のサンプリング周波数によって決まります。

図17a M:Lのサンプリング周波数変換システム

図17b LPFを1つにまとめたM:Lのサンプリング周波数変換システムのブロック・ダイヤグラム

図17c MDのサンプリング周波数（32kHz）をDATのサンプリング周波数（48kHz）に変換する回路

図17d DATのサンプリング周波数（48kHz）をMDのサンプリング周波数（32kHz）に変換する回路

サンプリング周波数変換技術の応用

　サンプリング周波数変換技術が実際の処理に立つ実例を1つ紹介します。サンプリング周波数8kHzでA/D変換した信号の成分をFFT分析することを考えましょう（図18a）。FFT長を512pointとすると、FFT分析の周波数分解能は8000/1024≒8Hzとなります。ここで周波数0〜1kHzの帯域だけを周波数分解能を上げて分析するにはどうしたらいいでしょうか？

　最も単純な方法はFFT長を長くすることです。例えばFFT長を8192pointとすれば、周波数分解能を8000/8192≒1Hzに改善することができます。しかしサンプリング周波数変換技術を用いればFFT長を512pointとしたままで高分解能の分析をすることが可能です（図18b）。

図18a FFT分析（分解能8000/1024≒8Hz）

図18b デシメーションを用いたFFT分析（分析帯域0〜1kHz、分解能2000/1024≒2Hz）

図18c デシメーションを用いたFFT分析（分析帯域2〜3kHz、分解能2000/1024≒2Hz）

　図18bでは、デシメータを用いてサンプリング周波数を2kHzに変換してからFFT分析を行っていますから、周波数分解能は2000/1024≒2Hzとなります。FFT長が短くて済むだけではなく、FFTの演算を行うときのサンプリング周波数が低くて済むというメリットもあります。

　ところで、よく考えてみると周波数帯域0〜1kHzの信号のFFT分析をするならばサンプリング周波数は2kHzで必要十分なので、最初から2kHzでA/D変換すればサンプリング周波数変換をする必要などないということになります。では、ある信号の周波数帯域2〜3kHz、あるいは3〜4kHzの成分をFFT分析する場合にはどうすればいいでしょうか？ この場合、サンプリング定理に従ってそれぞれサンプリング周波数6kHzと8kHzでA/D変換して分析するのが最適でしょうか？

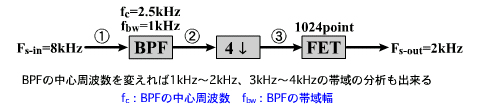
　サンプリング周波数変換技術を用いれば、より効率的な処理が可能です。例えば帯域2〜3kHzの成分をFFT分析するならば、図18cに示す方法で処理できます。

サンプリング周波数変換技術の応用

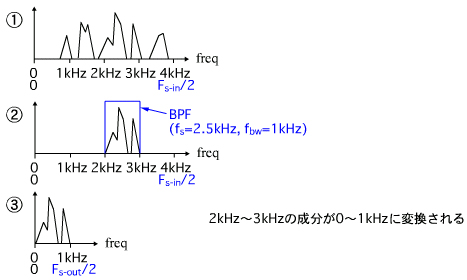
　図18cでは、デシメータの前にBPF（バンドパスフィルタ）があります。帯域幅は2〜3kHzですから、デシメーションすると2〜3kHzの周波数成分が折り返して0〜1kHzに現れることになります。

図19 デシメーションを用いたFFT分析（分析帯域2〜3kHz、分解能2000/1024≒2Hz）の回路でのサンプリング周波数変換の様子

　それをFFT分析すれば、2000/1024≒2Hzの周波数分解能で2〜3kHzの帯域を周波数分析できます。サンプリング周波数を用いることによりFFTのデータ長は短くて済みますし、FFTの演算をするときのサンプリング周波数も低くて済みますから、演算量削減の大きな効果を得ることができます。

　周波数帯域1〜2kHzの分析をする場合には、ページ図18cの回路のBPFの通過帯域幅を1〜2kHzに、周波数帯域3〜4kHzの分析をする場合には、BPFの帯域幅を3〜4kHzにすればいいことになります。ただし、この場合デシメーション後に0〜1kHzに現れる折り返し成分は元の信号とは周波数が反転したものになることに注意してください（変換前の3kHzの成分が変換後は1kHzに、4kHzの成分は0kHzになります）。

　このようにサンプリング周波数変換技術を上手に用いれば、広帯域の信号の任意の帯域幅を取り出して、少ない演算量で分解能の高い周波数分析をすることが可能となります。A/Dのサンプリング周波数は一定に保ったままで、デシメーションを用いたサンプリング周波数変換によりFFT分析処理は必要最小限のFFT長と必要最小限の低いサンプリング周波数で効率的に実行できます。

---

　次回は、引き続きDSPとほかのプロセッサの比較として、ASICとの違いをお話しします。