SPICEの過渡解析（その1）：キャパシタンス素子の場合：SPICEの仕組みとその活用設計（4）（2/3 ページ）

過渡解析とは、いわゆる時間的に変化する特性についての解析である。SPICEを用いた回路解析では、時間的に電圧や電流が変化する部品としては、キャパシタンス素子とインダクタンス素子がある。第4回では、キャパシタンス素子使う場合の過渡解析を取り上げる。

[加藤博二（Sifoen），MONOist]

キャパシタ（キャパシタンス素子）

　それではSPICEで使うキャパシタンス素子について説明していきます。

　いわゆる容量性素子のことでコンデンサとも言いますが、ここではキャパシタンス素子（キャパシタ）とします。

コンダクタンスの算出

　キャパシタCの電圧と電流の関係は式（5）で示されます。

図3　キャパシタの電流波形（クリックで拡大）

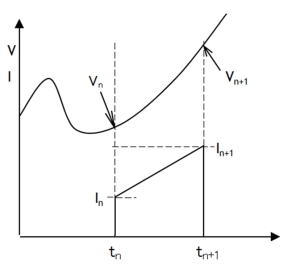
　この式の右辺は電圧の時間変化率を示しており、差分的に考えれば時間Δtに対する電圧変化をΔVとし、Δt→0とした時の値です。

　今、現在時刻をt_nとし、t_n＋1の時刻における電圧V_n＋1、電流I_n＋1を求めることを考えます。

　時刻t_n〜t_n＋1の区間の電流を陰解法の定義に従ってI_n＋1で代表すれば、I_n＋1は式（6）で計算することができます。

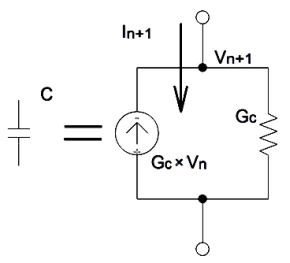
　コンダクタンスの単位は電流／電圧ですから、式（6）中のC／Δtはコンダクタンス単位となり、この値をG_Cとすれば式（6）は式（7）で表現できます。

図4　キャパシタ等価回路

　そして、式（7）を見ると、キャパシタの等価回路は図4に示すようにコンダクタンスG_Cと、I_n（＝G_C・V_n）という値の電流源から構成された回路ブロックと考えればよいことが分かります。

　式（7）においてはG_C、I_nが既知ですので、この回路構成を用いて次ステップの予測電圧V_n＋1を節点1の電圧として求めることができます。

　そして、I_n（＝G_C・V_n）、つまり初期値を変えると計算結果も変わってしまうことも分かります。

　ですから、次回説明するインダクタンス素子の場合も同じですが、t＝0での初期値は決してツール任せにはせず、設計者が意識して決めてやる必要があるのです。