SPICE応用設計（その6）：W.C.解析の注意点：SPICEの仕組みとその活用設計（17）（1/4 ページ）

今回はLTspiceを用いてワーストケース解析のもう1つの手法であるランダム偏差法について簡単に説明します。基本的な考え方はLTspiceでのモンテカルロ解析の応用と考えれば良いでしょう。

[加藤博二（Sifoen），EDN Japan]

　今回はワーストケース解析のもう1つの手法であるランダム偏差法についてLTspiceを用いて簡単に説明します。基本的な考え方はLTspiceでのモンテカルロ解析の応用と考えれば良いでしょう。

　また、前回の感度解析法、今回のランダム偏差法などのワーストケース解析では見落とされがちな課題と注意点について説明します。

ランダム偏差法を用いたワーストケース解析（LTspiceでの実施例）

1）　最初に関数定義コマンドを使ってワーストケース関数wcを次のように回路図上に定義します。

.function wc(nom,tol) if(i==0, nom, if(flat(1)＞0,nom＊(1＋tol),nom＊(1−tol)))

注)文頭の"."はコマンド文であることを宣言します

　関数の意味は

【1】引数はnom（定格値）、tol（偏差）の2つ。
【2】カウンター指数iがi==0、つまり初回計算時は標準(nom)状態です。以後は
【3】flat関数が>0なら偏差は(1+tol)、つまり上限に設定し、
【4】flat関数が=＜0なら偏差は(1-tol)、つまり下限に設定する。

ということです。
（flat関数とは引数を±範囲とする一様分布関数です）

図1　LTspiceでのwc関数使用例

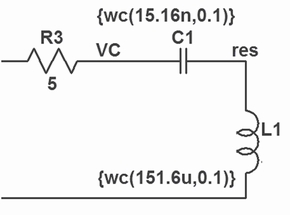
2）　図1に示すように、偏差を持つN個の部品の値の欄に{wc(15.16n,0.1)}のように、定義したwc関数で定格値と偏差を与えます。ここで{ }は"計算しなさい"という意味になります。

3）　試行回数を.STEP PARAM I=0 64 1のように回路図上で指定します。Iはカウンタで、0から開始しないと標準状態を計算しません。

4）　試行回数はN個の部品の上下限の全ての組み合わせを漏れなく含む必要があります。

　単純に計算すると必要な試行回数Mは　M＝（2^N＋1）

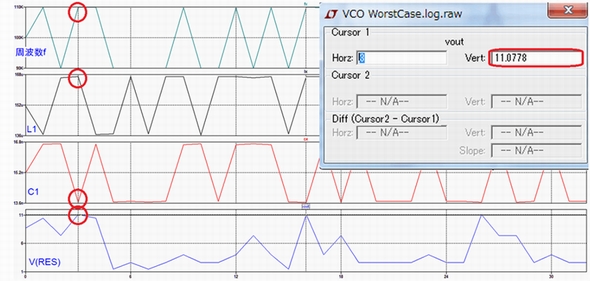
で求めることができますが、これは組み合わせに重なりがない時のもので実際にはflat関数でも2〜3回連続で同じ極性の値が出ることはありますし、実際に図2の実施例ではL1の値に最大7回程度の連続が見られます。

図2　LTspiceのワーストケース解析実施例 （クリックで拡大）

　また、図2では実際に64回試行して最大値は4回出現し、その最長の間隔は33回です。つまり試行回数Mとして33回の計算は最低必要だということです。

　この例から考えると実際の試行回数Mは最低限度、

　M＝（4×2^N）＋1　　　　　　…1式

程度は必要でしょう。

　したがって、感度解析法が『試行回数Mが部品点数Nに比例して直線的に増加』するのに対して、ランダム偏差法は『2のN乗に比例して試行回数Mが増加する』ことになり、実用的には小規模な解析にしか使えないということになります。

　また、このようなユーザー定義によるランダム偏差法を用いる場合はツールの標準機能と異なり最悪値が出現した時の回路条件を読み取ることができません。

　ですからこの手法を用いる場合にはモンテカルロ解析の時と同様に、MEASURE文（測定コマンド）を使ってその時々の回路条件を記録し、後から最悪値が出現した試行回数を読み取るようにコマンドを工夫する必要があります。

　ただ、残念ながら前記のwc関数定義ではLot変動とDev変動を個別に設定できません。ユーザー定義関数にもう一工夫必要なようです。