Spiceの新しい応用解析：自然対流問題（その2）：SPICEの仕組みとその活用設計（20）（2/3 ページ）

CFDツールでなければ解けない自然対流問題に適用できる熱抵抗回路網法ですが、単にSpice回路網上で実現させてもうまく動作しません。今回はいかに動作させるか、そして完成した回路の精度と妥当性について検証を行います。

[加藤博二（Sifoen），EDN Japan]

ユーザーインタフェース

　いくら計算が簡単でもデータの記述が難しいものであれば使い勝手は悪くなりますし、実行のたびに回路のアチコチに存在する定数を書き換えていたのではこれも都合が悪いものになります。基本的な回路図を変更なしで実行でき、実行時に簡単に数字を設定できる方法が良いでしょう。

　そのような要求を満たすものとして、Spiceには「PARAM」関数があります。

		単位
寸法	縦	mm
	横	mm
	厚み	mm
周囲温度 Ta		（℃）
放射係数 ε		（無次元）
表3 ユーザー設定項目

　これは変数表記したデバイスの定数をユーザーが数値入力するもので、今回の目的に使えます。

　損失は電流源の値として回路図にて設定しますのでユーザーが設定しなければならない項目は表3の通りです。

　本来ならSI単位系に基づいてMKS単位で規定しなければならないのですが、電子機器ではまだまだミリ寸法が一般的なのでこのような入力単位とし、モジュール内部でメートルに換算すれば良いでしょう。
温度についても入力は[℃]単位とし、内部で絶対温度に換算することにします。

実際の解析に当って

　解析の都度、図4の回路を回路図上に配置するのは非現実的ですし、間違いの元になります。また、結線は毎回同じですのでサブサーキットとしてユーザーから見えなくしても特に問題は生じませんし、使いやすさを考えればその方が便利です。

図5 実際の解析回路図

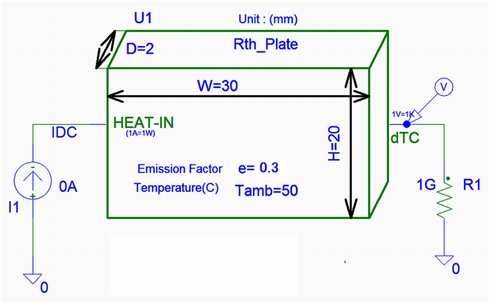
　このような考え方から、筆者の熱設計、電源設計などのセミナーで配布している熱解析モジュール（Rth_Plate.sub）はサブサーキット構成になっていますが、内部の回路構成は図4の等価回路と同じです。回路図上にシンボルを配置すると図5に示すように入力テーブルを組み込んだ外形が表示され、それぞれ必要な数字を入力できます。

　HEAT-IN端子は損失を与える端子で電流で損失を設定します。感度は1A＝1Wです。

　dTC端子は固体表面の周囲温度からの上昇値ΔTcを出力します。感度は1V＝1K(℃)です。

　内部計算は前述の通り、絶対温度で計算していますので出力する時に周囲温度との温度差に換算しています。