Spiceの応用解析――微分方程式を解く：SPICEの仕組みとその活用設計（22）（2/4 ページ）

今回は数値計算の代表的なツールであるSpiceの応用解析として、“アナログコンピュータ”を模擬して代表的な微分方程式を解いてみます。

LINE

Hatena

2階の微分方程式を解く

　今回対象とする微分方程式を4式に示します。

　この式の意味するところは
「原関数を2階微分したものは原関数f(t)に係数（－ω²）を掛けたものに等しい」
というものであり、振動方程式と言われるものを簡略化したものです。

　式が微分形式で記述されていますので5、6式のような積分形式に書き直します。

　6式において

を2重積分器の出力とすれば、2重積分器の入力信号はY"ですから、
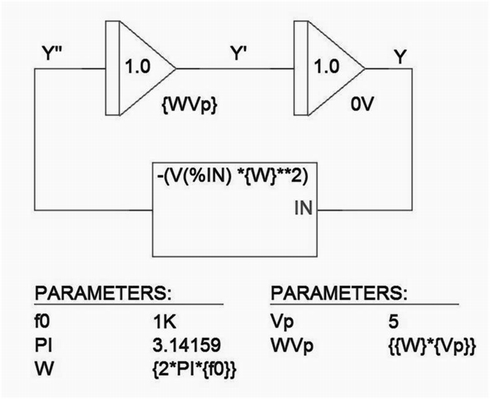
「2重積分器の出力(Y)に－ω²を掛けたものが積分器の入力信号(Y")になる」ように接続すれば良いわけです。この関係を図3に示します。（積分定数はそれぞれの積分器に初期値として設定します）

図3　6式の実行回路

　図3をみると、初段の積分器出力がY'、2段目の積分器出力がYになりますのでそれぞれの積分器の初期値は解曲線の傾斜（＝Y'）の初期値、解（＝Y）の初期値であることが分かります。

　Y'＝Y＝0とすると、Y'の積分値Yや微分値Y"はいずれも0となります。ですから関数の値は初期値から変化できず、水平軸を描きます。

　とりあえず、Y'≠0、Y≠0として仮解析を実行してみるとSin形状の波形を得ることができましたのでこの曲線を

図4　6式の実行結果

Y(t)＝f(t)＝V_P・Sin(ωt＋θ)　　　　 …7式

と表します。また、この関数の導関数は

f'(t)＝V_P・ω・Cos(ωt＋θ)　　　　　…8式

f"(t)＝-V_P・ω²・Sin(ωt＋θ)　　　　…9式

ですから、前述した4式の条件を満たしていることが確認できます。

　関数の基本形を確認するために図3において初期値Y(0)を0(θ＝0)、
そしてY'(0)＝f'(0)＝V_P・ωをY'の初期値に設定します。

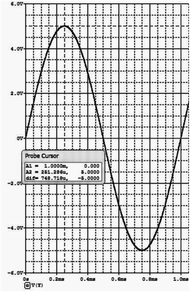
　図4はf₀＝1KHz,V_P＝5V_Pとして各定数を設定したものですが、再現結果は良好です。