ラプラス素子(その2):SPICEの仕組みとその活用設計(24)(2/4 ページ)
ラプラス素子はSpiceツールベンダー各社の独自拡張機能であり、ツール毎に振る舞いも多少異なります。そこで、今回はV&Vの観点で各ツールのラプラス素子の振る舞いについて見ていきます。
過渡応答の妥当性検証
このインパルス応答波形を利用して伝達関数を含むAC解析用の回路図で過渡解析も行えることは前回説明しました。いわゆる、畳み込み積分によるラプラス逆変換機能です。しかし、この畳み込み積分で使用する応答波形は上記説明から分かるように離散的なものですのでいくつかの設定可能な項目と精度の関係を事前に調べておく必要があります。
今回、手元にあるラプラス素子の使えるいくつかのSpiceを使って1次遅れ回路、2次遅れ回路、および(1−S)回路における過渡応答を検討しました。その結果を表1、表2、表3に示します。
注)下記の結果は筆者のツールのバージョンや解析環境の影響も含まれています。ラプラス素子の使用に当っては必ず各自で事前に確認をしてください。また、ラプラス素子の設定条件は断りがない限り、全て初期値のままです。
1次遅れ回路
1次遅れ回路とは前出の図1で取り上げたような回路であり、回路の出力信号の位相回転が−90°になるものです。具体的にはR-C回路やL-R回路で構成する1段のローパスフィルタ回路が該当し、その伝達関数の基本の型は1式になります。
評価に用いた図1の回路例ではα=1です。この回路例での検討結果を表1に示します。
結果の要約
初期の期間は各Spiceとも正常に応答し、精度も0.4%程度が得られていますが時間が経過しますとTopSpiceのみ8秒以後に振動を生じました。
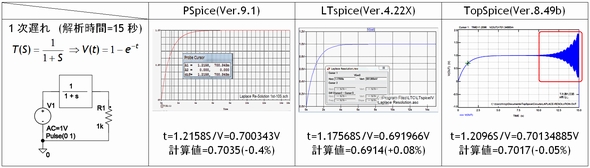
表1 1次遅れ回路の評価結果 (クリックで拡大)
注)一部のSpiceのラプラス素子は後述するようにnfft項、他を設定することで特性を改善できるのですがここでは前述の通り初期値のままとしてあります。
表1の1次遅れ回路の時定数が1秒なので計算点を十分に(例えば100点/秒)確保するため、過渡解析の最大TimeStepは10mSとしました。この値は2次遅れ回路と共通です。
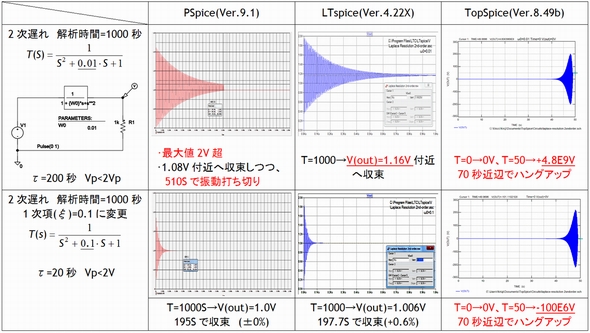
2次遅れ回路
2次遅れ系とは出力信号の位相回転が−180°になるもので、2次のフィルタ特性や多くの制御系の基本応答特性となるものです。
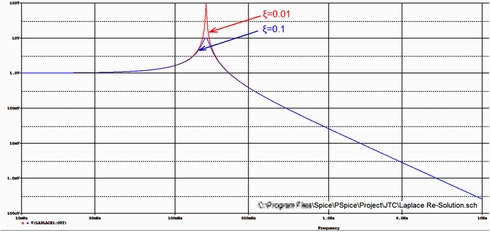
この系の代表例として図3に示す2つの特性(ξ=0.1/0.01)の振動型2次遅れ回路について評価しました。
伝達関数の型は次のようになります。
ξ:曲線のピークの鋭さを左右するパラメータです。一般的には"S2+2・ξ・S+1"の型で表現されることが多いのですが、これは分母の2次式の一般解との関係によるものです。特に意味がありませんのでここではξ・Sの型で表現しました。
このタイプの評価結果の詳細を表2に示しますが要点は以下のようになります。
ξ=0.01 (理論解:減時定数τ=200秒)
PSpice
最大値が2Vpを超え、また510秒付近で1.08Vを中心に振動していた振動波形がいきなり停止しました。振動が打ち切られた後の安定値は1Vであり、なぜか安定値そのものは正しく計算されていました。
LTspice
収束値が1.16Vと理論値からズレてしまいました。
両者とも正しい波形を得ることはできませんでした。
ξ=0.1(理論解:減衰時定数τ=20秒)
1次の係数(ξ)を0.1とした場合には両者とも0.6%以内の精度で答えを得ることができました。ただし、各設定条件によっては中村利男さんのWebサイトのようにξ=0.1でも差が生じる例も報告されていますので過渡応答波形を求める時には理論解が分かっている波形で応答を事前に確認しておいた方が良いでしょう。
中村利男さんのWebサイトによりますと、次のような場合に問題を生じるそうです。(青字は筆者加注)
(1)周波数応答係数が収束しない場合(インパルス応答が解析時間内に十分減衰しない)
(周波数をあげても、係数の大きさが無視できる程度に小さくならず、逆フーリエ変換を行う最大周波数が規定できない場合)
(2)インパルス応答が振動的で収束しない場合(振動減衰時間が解析時間に対して無視できない場合)
(畳み込み積分の積分範囲が規定できない場合)
その他にも伝達関数が次の型の場合には入力波形によって不安定になります。
伝達関数の型が1/(S2+ω02)になるような関数(Sin、Cos関数でありξ=0に相当)の場合
Copyright © ITmedia, Inc. All Rights Reserved.