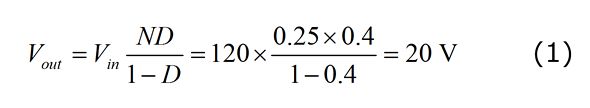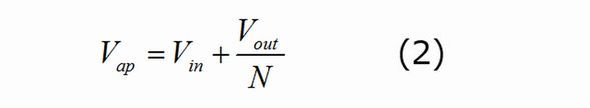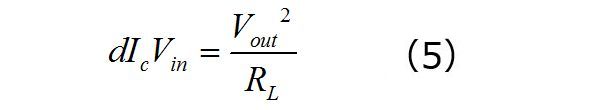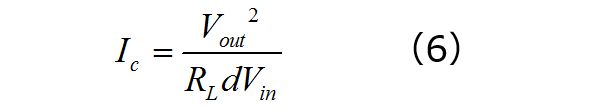漏れインダクタンスを使用したフライバックコンバーター（2） 平均モデル化：電源設計（2/4 ページ）

本連載の第1回では、漏れインダクタンスによってもたらされるスイッチング効果について説明しました。実効デューティ比の低下により、2次側ダイオードの導通時間が長くなり、メインスイッチがターンオフした後、2次側電流が変化するまでの遅延が発生します。その結果、元の式による予測値よりも出力電圧が低くなり、RCDクランピングネットワークでの消費電力が増加します。動作波形において漏れに関連する項が及ぼす影響を考慮した場合、フライバックコンバーターの小信号応答に与える漏れの影響を検討するのは興味深いことです。ただし、小信号分析を実行する前に、適切な平均モデルが必要になります。

[Christophe Basso（ON Semiconductor France SAS），EDN]

フライバックコンバーターをシミュレートする方法

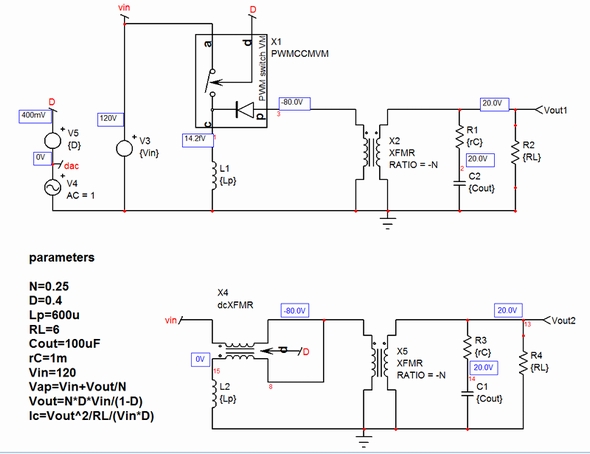
　図5に、PWMスイッチモデルを使用してフライバックコンバーターをシミュレートする方法および、比が1：dである特殊なトランスを使用した等価回路を示します。長方形の枠で囲まれた電圧はシミュレーターが計算したバイアスポイントです。これらの電圧が適切な制限範囲内に収まっていることを確認することが重要です。時には、ソルバーが適切な動作ポイントの決定に失敗することがありますが、その場合でも動的応答は利用できます。この応答は明らかに誤った結果であり、正しい動作ポイントが新たに見つかるまでは、それを廃棄する必要があります。第1回から、完全な（漏れインダクタンスのない）CCMフライバックのDC伝達関数が次の通りであることが分かっています。

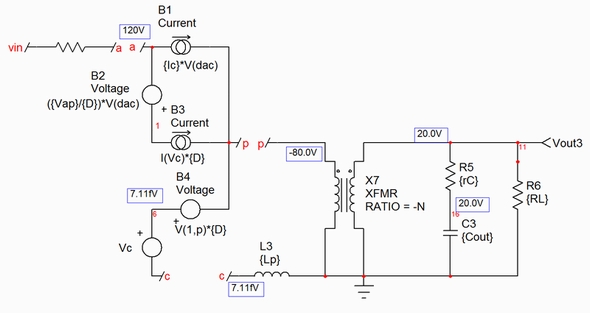
　これは回路図が負荷抵抗の両端間で示す値です。この例のバイアスポイントは正しいポイントです。ここまでで大信号モデルが確定しました。図4に示した回路図に基づく小信号の実装を明らかにできます。この目的で、いくつかの固定パラメーター、つまりV_apと端子「c」における平均電流I_cを計算する必要があります。PWMスイッチモデルを流用してフライバックコンバーター構造に当てはめた後、端子「a」と「p」の間の電圧であるV_ap,は、入力電圧V_inから反射電圧V_out/Nを引いた値に等しくなります（2次側ダイオードのV_fを無視）。後者の電圧は負の値なので、次式を導くことができます。

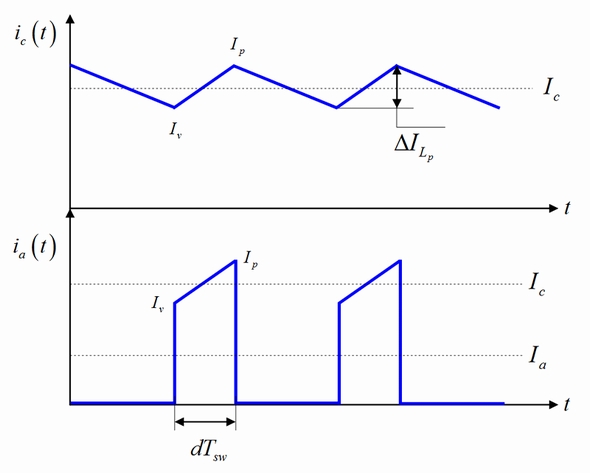
　端子「c」を流れる電流は、1次側インダクタンスL_pに流入する平均電流に等しくなります。この電流のうち一部は、オン時間つまりdT_swの期間は端子「a」に向かって流れ、オフ時間つまり（1-d）T_swの期間は端子「p」に向かって流れます。図7に端子「a」と「c」の代表的な瞬時波形を示します。図5に示すアプリケーション回路図から、端子「a」の平均電流は入力信号源にも流れ、P_inを形成することが分かります。

図5：CCMフライバックコンバーターでのPWMスイッチモデルの実用的な実装 （クリックで拡大）

図6：PWMスイッチモデルの小信号バージョンは少数の制御信号源のみ必要 （クリックで拡大）

図7：端子「c」に流れる電流は1次側インダクタンスLpに流れる電流に等しい （クリックで拡大）

　図7から次式を導けます。

　式（3）に式（4）を代入し、100％の効率（つまり、P_in＝P_out）を想定すると、次式が得られます。

　したがって、

となります。

　図5のパラメーターウィンドウを使用してこの式を評価し、パラメーターとして制御信号源に渡します（中カッコ内の値）。ここでシミュレーションを実行し、全ての曲線を共通のグラフ内に集約することができます。

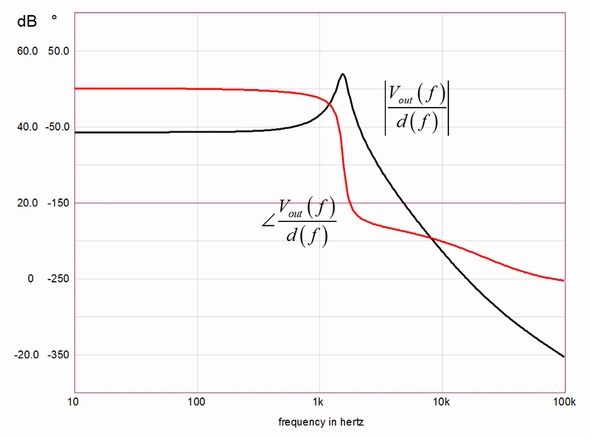
　集約の結果が図8であり、全ての曲線（振幅と位相）は正確に重ね合わせてあります。これはCCMフライバックコンバーターの従来よりみられる応答で、出力に対する入力のデューティ比に対応します。共振周波数でピークが形成されており、その後ESR（等価直列抵抗r_C）ゼロが登場し、続いてRHP（右半平面）ゼロが位相をさらに減少させます。

図8：3つの異なるモデル（カプセル化された大信号モデル、トランスベースの回路、線形化バージョン）を正確に重ね合わせて取得した周波数応答 （クリックで拡大）