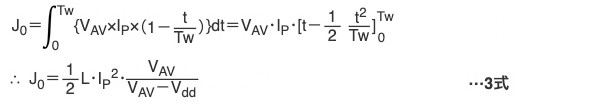半導体(9)―― MOSFETのアバランシェ耐量の使い方(II):中堅技術者に贈る電子部品“徹底”活用講座(68)(1/2 ページ)
今回はエネルギー吸収時のチャネル温度変化を説明するとともに、アバランシェ対応チップが持つ吸収エネルギー保証曲線について説明します。逆に言えば、ここで説明する保証曲線を持たない限りアバランシェ耐量に対応しているとは言えないことになります。
前回はMOSFET固有のアバランシェ耐量とは何か? について説明するとともにチップがアバランシェ耐量に対応しているか否かについて説明しました。
今回はエネルギー吸収時のチャネル温度変化を説明するとともに、アバランシェ対応チップが持つ吸収エネルギー保証曲線について説明します。逆に言えば、ここで説明する保証曲線を持たない限りアバランシェ耐量に対応しているとは言えないことになります。
アバランシェ耐量の試験方法
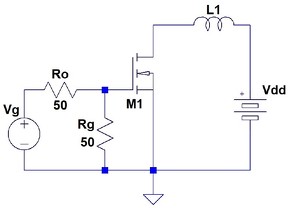
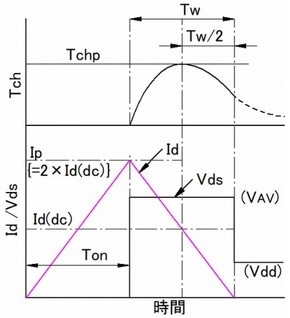
実際のアバランシェ耐量の保証はサージエネルギーをチップに与えて破壊の有無やダメージの有無をチェックすることで行われます。その試験回路の概要を図1に、また各部の波形を図2に記します。
アバランシェ状態に入る時のドレイン電流IARの保証値は一般的には定格ドレイン電流Id(dc)であり、大まかな試験の流れは次の通りです。
- 図1の回路においてId(dc)×2のドレイン電流(Ip)に達するまでMOSFET(M1)を通電させます。
- その後、M1を遮断してインダクタンスL1に誘起電圧を発生させます。
- 誘起電圧がVAVを超えると前回説明したアバランシェ動作によってM1がサージエネルギーを吸収します。
- このエネルギーによってM1のチャネルに損失が発生するのでチャネル温度は特有の温度上昇曲線を描いて上昇しブレークダウン期間(Tw)の中央でピーク(Tchp)に達します。
ブレークダウン期間(Tw)中の温度変動ΔTchは1式で計算しますが1式が成立するためには期間Twは過渡熱抵抗Rth(Tw)がTwの√に比例する時間域でなければなりません。Twの値は2式で計算できるのでカタログの過渡熱抵抗曲線から確認できます。
で表わした場合、
この時ドレイン電流は直線*を描いて減少していますのでId(dc)×2(=Ip)でスタートしたドレイン電流がId(dc)まで下がった時にピーク温度(Tchp)に達することになります(図4の計算式にδ=0を代入)。
このような試験条件にすることによってTch=Tch(MAX) 、Id=Id(dc)でのアバランシェ特性を保証することができます。試験でのピーク電流IPがId(dc)値の2倍になっているのは単なるマージンではなくこのような背景からなのです。ただし、アバランシェ特性を使用する時にはあくまでもTch<Tch(MAX)、Id<Id(dc)が保証条件になりますので保証範囲を逸脱しないように注意してください。
MOSFET(M1)に加わるエネルギー量J0はインダクタンスL1のエネルギー以外に電源Vddから供給されるエネルギーも含まれるので3式で計算します。
なおチャネル温度の上昇値は期間Twしか制御因子がありませんのでインダクタンスL1の値とVddで調整します。
図3はブレーク中のチャネル温度の変化の様子を計算したものですが時間が0.5の時にピーク温度に達していることが確認できます。なお図3はグラフの視認性を上げるためにパラメーターを設定していますので現実の値ではありません。
また参考までにハンドブックなどによく記載されている三角波状損失について温度上昇を計算したものを図4に記します。同じ三角波形状の損失でもピーク温度やピーク温度に達する時間は変動します。
簡易的には係数を2/3にしておけば問題はありませんが、そもそもこのような値を考慮に入れなければならないこと自体が「熱的マージンがないことの現れ」ですから使用条件を見直すことが先決です。
Copyright © ITmedia, Inc. All Rights Reserved.