ジャンクション温度の計算(1)―― 温度計算の原理:中堅技術者に贈る電子部品“徹底”活用講座(75)(1/2 ページ)
今回から、数回にわたり半導体を使う上で考慮しなければならない接合(ジャンクション)部の温度計算の算出法について説明します。
前回まで説明してきた半導体のワイヤーボンド技術は直接的に設計者が使い方を考慮できるものではなく、半導体メーカーの仕様に関するものです。半導体を選択する時やメーカーからの仕様変更の申し入れ、故障解析レポートの評価時などにおいてメーカーの情報のみで判断せず、一度立ち止まって評価内容について吟味する姿勢を忘れなければ良いかと思います。
今回から、数回にわたり半導体を使う上で考慮しなければならない接合(ジャンクション)部の温度計算の算出法について説明します。この接合部の温度は熱電対や熱画像などで測定できるものではありませんので理論に基づいた計算が一般に用いられます。
過渡温度上昇の影響
本稿では各種部品の構造や使い方について説明してきましたが半導体については使い方を特に説明はしませんでした。しかし半導体は使い方を誤ると破壊、焼損を引き起こしたり、そのレベルまでは至らないとしても部品の故障率に多大なる影響を与えます。そのため市場での品質やメンテナンスなどのサービスコストを考慮した機器の設計では設計資料の一環として推定故障率の算出を求められることも多々あります。
この故障率には電圧、電流、温度などのディレーティングが影響します。その中でも電圧、電流などはオシロスコープなどで波形として測定できるので過渡的な問題を見逃すことは少ないのですが温度については実測できるのは定常的なケース温度のみです。
故障率の算出にはチャネル(ジャンクション)の過渡的な温度も重要*なパラメーターなのですがチャネル温度の算出には過渡熱抵抗曲線を使った温度計算程度しか計算手法がなく、またその計算手法も半導体メーカーの技術資料に記載された代表的ないくつかの損失波形についてのものですので実際の故障率の推定には確信が持てませんでした。
ここでは過渡的な温度計算の基礎である「重ね合わせの理」に基づいて代表的な損失波形の温度上昇の計算の意味について考えていきます。
*半導体のチップ周辺にはチップ接合用はんだ、エポキシ成形樹脂、など温度によって寿命が変化する部品が多々あります。半導体においてはこれらの材料、特にエポキシ樹脂のガラス転移温度(TG)や各材料の線膨張係数に起因する熱応力などの観点から150℃をめどに使用温度の上限が定められています。この温度を超えると直ちに破壊するものではありませんが故障率は急激に増加し、寿命が著しく短くなります。
チャネル温度の実測
半導体、特にFETやバイポーラトランジスタなどのカタログには後述する図3に示すような過渡熱抵抗曲線と呼ばれる特性曲線が付属しています。この曲線は次の手順による実測結果と熱伝導理論に従って作成されていていますのでデータの信頼性は十分です。詳しくは検索サイトで「過渡熱抵抗」、「測定」などのキーワードで検索すれば容易に資料を入手できますが、ここではイメージだけを説明します。
①事前測定:恒温槽中に設置した、FETのボディダイオードのPN接合、あるいはバイポーラトランジスタのC-B間のPN接合を使って1mA程度の測定電流でVF-Ta曲線を事前に採取します。この時に接合部に発生する損失は1mW以下なのでパワーデバイスでは無視でき、Ta(周囲温度)=接合温度と見なせます。
[測定法A]
②-1 半導体を無限大ヒートシンクと見なせる水冷ヒートシンクに取り付けます。
②-2 接合部にパルス電流を流して規定の電力(W)を規定の時間(tW)発生させ、
直ちに①で設定した測定電流まで低下させます。
②-3 接合部のVFを測定し、VF-Ta曲線から接合部の温度を測定します。
ただし、この測定法は短パルス領域の損失波形の精度やVFの測定精度が悪く近年では次の手法が用いられます。
[測定手法B]
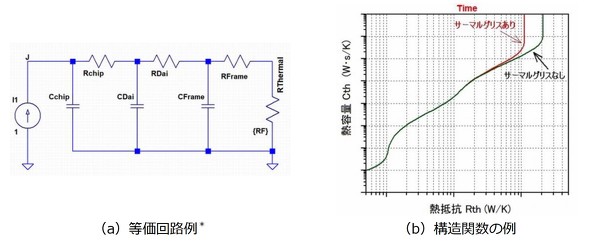
図1に示すこの手法は2010年にJEDEC*で規定された方法でJESD51-14として標準化されています。この手法には後述する「重ね合わせの理」が使用されています。
③-1 半導体を無限大ヒートシンクと見なせる水冷ヒートシンクに取り付けます。
③-2 接合部に発熱用電流を流して接合部を所定の温度(Tj(MAX))まで上昇させ、
温度飽和させます。
③-3 温度飽和後、発熱用電流を瞬時に測定用電流(1mA)まで低下させ常温に戻る
までの期間、時間とVFの関係を測定します。
③-4 VFを①のVF-Ta曲線と照合して接合部温度(Tch)を算出しTch-Time曲線を
得ます。
③-5 熱が流れる各部は熱容量の違いからそれぞれ独自の熱時定数を持ちますので
Tch-Time曲線は熱時定数に基づく固有のうねり方をします。
③-6 このTch-Time曲線のうねり方から熱の流れる領域の構造関数を算出し、
この構造関数から接合部、チップ部、ダイボンド部(はんだなど)、
フレーム、サーマルグリス、などの熱抵抗を算出します。
特に5、6の項目は不良品と良品を比較することで損傷を内包した箇所を特定できます。図1(b)ではパッケージ裏面に塗布するサーマルグリスの有無によって構造曲線が変化する様子を示していますが開封せずに行うチップクラック、ダイボンド(ソルダー)の剥がれなどの故障解析としても有効です。
発熱を中止することで過渡熱抵抗が測定できることを不思議に思われるかもしれませんが損失PDを0にすることは0=PD+(−PD)ということであり、「重ね合わせの理」によればーPDの損失を追加で発生させるという意味になります。温度変化はそれぞれの変動が独立していますのでこの測定法でPDに対する過渡熱抵抗を算出することが可能になります。
注)測定法A、Bの注意点としてパッケージを水冷ヒートシンクに取り付けていますので取り付け面全体から熱が伝わっています。このため図1(a)に示すような、あるいは熱電対で測定できるような特定の測定箇所ということは正確には定義できません。熱電対などでケース温度(TC)を測定した場合には若干とは言え誤差が含まれることになります。
一般的にはTCとしてチップ搭載位置のパッケージ裏面(取り付け面)のヒートシンクに穴を開けて熱電対を挿入し、測定された温度を使用しますが簡易的にパッケージ表面に貼り付けた熱電対や赤外線画像から得られた温度を使用する場合は10%程度の誤差を見込んでください。
*Joint Electron Device Engineering Council
EIA(米国電子工業会)の下部組織で半導体や電子部品の標準化を行っています。
Copyright © ITmedia, Inc. All Rights Reserved.