ジャンクション温度の計算(3)―― 任意の三角形損失の温度計算:中堅技術者に贈る電子部品“徹底”活用講座(77)(1/4 ページ)
今回は「重ね合わせの理」を使用して増加形三角形の損失波形を任意の三角形の波形へ拡張することを考えていきます。
前回は「重ね合わせの理」と45°熱拡散モデルを使って基本となる増加形三角形の損失波形について計算式を検討しました。その結果、ハンドブックなどに記載されている近似係数の0.669は波形を200程度に細分化して計算したものと推測できることが分かりました。なお、本稿ではこの近似係数を温度上昇係数と称します。
今回はこの重ね合わせの理を使用して増加形三角形の損失波形を任意の三角形の波形へ拡張することを考えていきたいと思います。
今回もいくつかの数式が登場しますが、できる限り詳しく式について説明しますので繰り返し読んでいただければ話の流れは理解できると思います。
損失が一定値から単純減少する場合
いきなり任意形状の三角形損失への拡張は計算式の説明や理解が難しくなります。ここではその前段階として計算手法の確認と計算の流れを把握するためにアバランシェ損失について考えます。
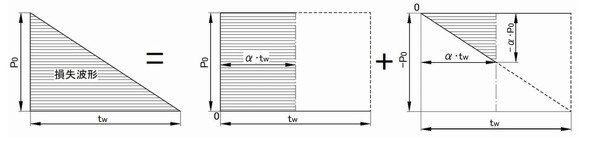
この損失波形は名前の通り、パワーMOSFETのアバランシェブレーク(降伏)のように波形の初期に最大損失が発生し、以降は順次直線的に損失が減少する、いわゆる図1の降下形三角形の損失波形を意味します。
この損失波形は図1に示すように重ね合わせの理を使って損失P0の矩形波の損失と、ピーク損失(−P0)の負の三角形の損失が重なったものとして計算します。
負の損失の場合、温度が時間とともに降下します。図1の波形例では矩形波損失の温度上昇と三角形損失(負)の温度降下が打ち消し合うので無条件で最大温度上昇が波形後端部に存在するとは言えません。実際に計算して時間tと最大温度上昇の時間の関係を確認する必要があります。
このため計算時間tと損失発生期間tWの比率としてパラメーターα(α=t/tW、α=0〜1)を定義します。
1)矩形波の損失による温度上昇ΔTrecは√(t)に比例しますので1式で計算します。
ここで計算時間tはt=α・tWです。
2)負の三角形の損失による温度上昇ΔTtriは損失も時間依存性(P=−α・P0)を持つことを考慮して2式で計算します。
3)総合温度上昇ΔTはΔTrecとΔTtriの合計値ですから3式になります。
4)この3式を見ると温度上昇ΔTはαの依存性を持つことが分かります。このΔTが最大になるα(変曲点)を求めるために3式の1次の微係数が0になるαを求めます。
この結果から温度上昇は減少途中の波形中央で最大になることが分かります。この時の温度上昇ΔTは3式のαを0.5とした4式になります。
[分割数の影響]
前回説明したように分割数が少ない(粗い)場合の増加形三角形損失の温度上昇係数は2/3より大きくなります。
ですから今回の例のように増加形三角形の損失で打ち消した場合、分割数が粗いと打ち消しが過大になるので総合の温度上昇係数は分割数の増加に従って0.471より小さい側から漸近していく様を示します。
例えば10分割では0.442、20分割では0.456程度を示し0.471より大きくなることはあり得ません。
しかし、ハンドブックによってはこの温度上昇係数について0.473などの値を採用しているものもあります。このような値となった背景には三角形損失の温度上昇係数が2/3ではなく、0.664〜0.665程度になっていることが考えられます。
この値は分割数N=20の中点法を使った三角形損失の温度上昇係数0.6644と類似であり、このことからこのハンドブックの例ではこのような計算手法が用いられたものと推定できます。
しかし多くの設計で参考にされるハンドブックは理論に裏付けされた資料であるべきであり、少ないけれども誤差を含んだ式が記載されることは好ましくありません。
Copyright © ITmedia, Inc. All Rights Reserved.