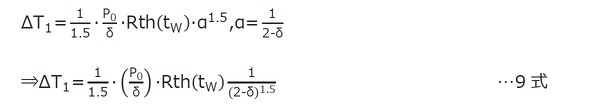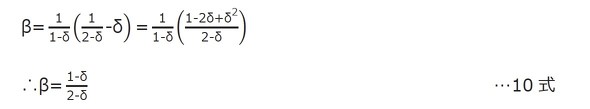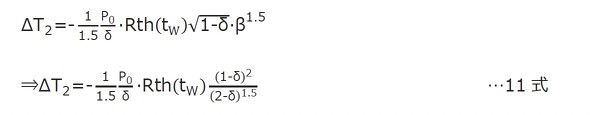連載
ジャンクション温度の計算(3)―― 任意の三角形損失の温度計算:中堅技術者に贈る電子部品“徹底”活用講座(77)(3/4 ページ)
今回は「重ね合わせの理」を使用して増加形三角形の損失波形を任意の三角形の波形へ拡張することを考えていきます。
損失波形が任意の三角形の場合の最高温度上昇値
最高温度に達する時刻αが8式で求まったのでこのαを各計算式に代入します。
1)基本損失による温度上昇ΔT1
5式のαに8式を代入します。
2)打ち消し損失による温度降下ΔT2
ですからこの式に8式のαを代入します。
10式のβを6式に代入します。
3)ΔT1とΔT2を合算し、総合温度上昇ΔTを求めます。
まず分子を計算し、その結果を代入します。
注)9式、11式ではδ=0で計算が破綻しますが総合温度上昇の12式ではδが打ち消しあって値を求めることができます。
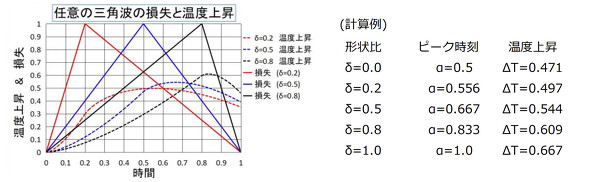
参考としてP0=1、Rth(tW)=1とした時の様子を図3に示します。
Copyright © ITmedia, Inc. All Rights Reserved.