ジャンクション温度の計算(5)―― 繰り返しパルス列の温度計算:中堅技術者に贈る電子部品“徹底”活用講座(79)(1/2 ページ)
これまで、各種形状の単パルス損失が発生した時の温度上昇の求め方について技術的な検証を含めて説明してきました。ただ、実機においては単パルスではなく同じ損失が繰り返し発生します。今回はこの繰り返し損失波形の温度上昇について考えていきます。
前回までは各種形状の単パルス損失が発生した時の温度上昇の求め方について技術的な検証を含めて説明してきました。この章の目的は最終的には実機の過渡温度上昇を求めることにありますが実機においては単パルスではなく同じ損失が繰り返し発生します。今回はこの繰り返し損失波形の温度上昇について考えていきます。
繰り返しパルス列の温度計算
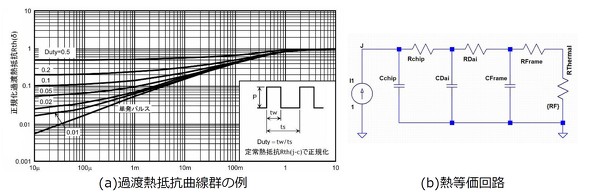
市販されている多くのパワーMOSFETのカタログには図1(a)に示すように、「矩形波状、最大損失P、パルス幅tw、周期ts」の繰り返しパルス列が加えられた時の印加時間比率(δ)と熱抵抗Rth(δ)の関係が過渡熱抵抗曲線として表記されています(δ=tw/ts)。
MOSFETの熱等価回路は図1(b)に示すように複数の熱時定数を持つ構造として表現できます。この回路構成はローパスフィルターですのでパルス周期(ts)がカットオフ時定数よりはるかに短い(45°モデルが成立する)場合、温度上昇は“DC成分に相当する定常的な成分+フィルタリング(減衰)された高周波変動”が重畳されたものとして考えることができます。
この定常解に相当する成分(DC解)では熱時定数回路は全て安定状態に達していますので平均損失P(δ)とRth(J-C)のみが温度上昇(=熱抵抗)を左右します。
つまり、1式で表されるDC成分に該当する平均損失P(δ)が温度上昇を左右するパラメーターになります。
本稿では矩形損失を最大値(P)で正規化しているため、1式は等価損失の減少を熱抵抗の見かけの減少として表現していることと等価になります。
この結果、熱抵抗の時間依存性はパルス幅の短い(左側)領域から順にδ×Rth(J-C)〜Rth(tw)〜Rth(J-C)で成す右肩上がり(↗)の階段状となります。
[詳細過渡熱抵抗曲線]
図2は繰り返しパルス列中の温度変化を求めるために損失を重ね合わせの理に従って分解したものです。
以下の項では最大損失P、印加時間tw、繰り返し周期ts、損失印加時間比率δとします。
①平均損失δ・Pが定常的に印加されδ・P・Rth(J-C)の温度上昇が発生しています。
②ある時刻からP(1−δ)の損失が①の結果に重畳されます。この結果、合算損失は+Pになります。
③twの時間経過後、等価損失を0に戻すために−Pの損失が重畳されます。
④1周期(ts)経過後、今度は+Pの損失が重畳されます。
⑤tw経過後、再び−Pの損失が重畳され等価損失は再び0になります。
⑥このようなサイクルが繰り返され最後に+P、時間twの損失が発生した時の合算温度上昇が求める温度上昇になります。
このような考え方に基づいて温度上昇の計算式を考えます。ここでは時間はtw、損失は+P、熱抵抗はR0・√(tw)で式を正規化します。したがってtw=ts×δ⇒ts=tw/δですからtw=1、ts=1/δです。またパルス数nのカウントは図2から分かるように0からスタートしています。
①の温度上昇ΔT1は既に説明したように2式です。なおRth(J-C)は正規化していません。
②最初の損失変化は損失を+1にするために(1−δ)を加えます。印加時間はn・ts+twですから温度上昇ΔT2は3式になります。
③損失を0に戻すため-1の損失をn・tsの期間にわたり加えます。したがって温度上昇ΔT3は4式になります。
④再び損失を+1にするため(n−1)ts+twの期間、+1の損失を加えます。
⑤再度、損失を0にするためにtw経過後に(n−1)tsの期間−1の損失を加えます
⑥このような繰り返しの最後に+Pの損失がtwの時間発生し温度上昇ΔT6を生じます。
パルス列による温度変動分ΔTは定常(DC)的な温度上昇ΔT1を除いたΔT2〜ΔT6までを合算した値ですので8式で求めることができます。
例として最初のパルス(n=0)による温度上昇は1パルスだけの成分による9式になります(定常温度上昇ΔT1は除いています)。
一方、多くのハンドブックでは繰り返しパルス列の温度計算では定常的な成分に加えて2回のパルス印加を考慮するように提言しています。提言に従って実際に2回目のパルス(n=1)を考慮した場合では繰り返し成分による温度変動ΔTは10式になります。
Copyright © ITmedia, Inc. All Rights Reserved.