ステップダウン形DC/DCコンバーターの設計(1):たった2つの式で始めるDC/DCコンバーターの設計(3)(1/3 ページ)
今回はこれまで説明した2つの式を使って基本的なステップダウン形DC/DCコンバーターを設計していきます。また最後に前回の課題の1つの考え方を示します。
前回は本連載「2つの式」の中で残ったCの式について説明しました。その中でキャパシターについて理解を深める意味で課題も出しました。答えが正しくなくても考えることを通じて理解が進めば課題を出したかいもあります。
今回はこれまで説明した2つの式を使って基本的なステップダウン形DC/DCコンバーターを設計していきます。また最後に前回の課題の1つの考え方を示します。
今回から数式がしばしば出てきますが式の成り立ちは今まで説明してきたLやCの基本特性を使って電圧、電流の波形を数式で表したものです。
数式と電圧、電流波形を対比してもらえばきっと数式の意味を理解できるはずです。
諦めずに筆を進めてみてください。
ステップダウン形DC/DCコンバーターの設計
特に注釈がなければ本稿では次の用語をコンバーターの状態を表す用語として共通的に使用します。
f:DC/DCコンバーターの動作周波数 tS:1周期の時間(=fの逆数) tS=ton+toffです。
ton:FET-SWが導通している時間 toff:FET-SWが遮断している時間
δ:tonがtSに占める割合(オン時比率) したがってton=tS×δ、あるいはδ=ton/tSです。
1. 基本回路の動作
図1(a)にステップダウン形DC/DCコンバーターの基本回路を示します。動作解析のためにこの回路をFETスイッチS1とダイオードスイッチS2を用いて図1(b)のようにモデル化します。
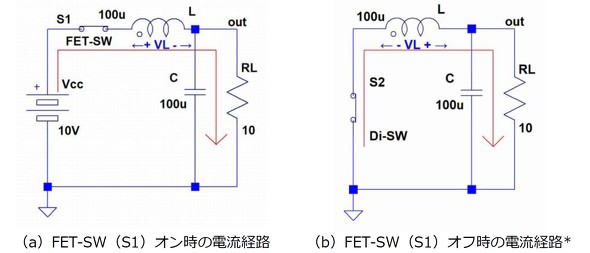
さらに回路図をFETスイッチS1のオン時とオフ時に分け、図2のように回路を分けて考えます。
[図2(a) FET-SW オン時]
FET-SW(S1)のオン期間中は図2(a)に示すように電流経路で一番高電位の電源VccからスイッチS1、インダクターLを介してキャパシターCと負荷RLに電流が流れます。キャパシターCには疑似定電圧性がありますので発振周期tsの時間範囲内では定電圧源と見なすことができます。この結果インダクターLに印加される電圧VLは“V-V(out)”の一定電圧になります。ここでVは電源Vccの電圧、V(out)はout端子の電圧です。
この電圧によるインダクター電流の増分ΔI(ON)はLの式(ΔI=(E/L)・Δt)を適用すると1式になります。
この電流増加によってインダクターLの蓄積エネルギーは増加し、増加したエネルギーは電源の供給がなくなる次のオフ時に負荷に放出されます。
このようにインダクターを使用するとインダクターLにエネルギーが蓄積されるのでキャパシターCへの充電電流の急激な変化が抑えられ電流変化が緩やかになります。インダクターをこの目的で使用する場合、このインダクターをチョークコイル(Choke Coil/塞流線輪)、あるいは単にチョークと呼びます。
[図2(b) FET-SW オフ時]
所定の時間の経過後にFET-SWがオフして外部からの電源供給がなくなってもチョークLには電流連続性がありますのでオン時と同じ方向に電流が流れ続けようとします。その結果チョークLの誘起電圧VLの極性は図2(b)に示すように反転し、チョークはエネルギー供給源として動作します。
結果としてオフ期間中はエネルギーが蓄積されたチョークLから図2(b)の方向でキャパシターCへ電流が供給され続けます。
この電流によってチョークLから負荷RLへエネルギーが移りますので時間と共にチョークLのエネルギーは減少し、このエネルギーの減少に従ってインダクター電流は減少します。
この時、発生する電圧VLの大きさは図2(b)から分かるようにキャパシターの疑似定電圧性によって出力電圧V(out)に等しく*なります。
*インダクターは疑似定電流性ですから発生電圧は疑似定電圧性を持つキャパシターの電圧に固定されます。
またオフ期間中は図1(a)や図1(b(のFET(M1)、あるいはFET-SW(S1)が遮断状態ですのでこの電流[ΔI(OFF)]は電流経路がダイオード(M1)やDi-SW(S2)に切り替わって流れます。このようにオン時とオフ時では電流の流れの一部が切り替わります。この電流の切り替わりや前述したチョークLの誘起電圧の反転が後で述べるDC/DCコンバーターのノイズ発生の源になります。
電流の変化率はLの式(ΔI=(E/L)・Δt)を適用すると
です。
またtoff期間中は前述したようにインダクターLのエネルギーが減少します。このためΔI(OFF)は減少する方向となります。
*図2中のVLの極性はキャパシターC側を基準電位にしています。2式の負記号は図2(b)のVLの極性が反転していることを示しています。
Copyright © ITmedia, Inc. All Rights Reserved.