発振器の周波数を1個の可変抵抗で変える：Design Ideas アナログ機能回路

正弦波発振器の課題を解決する回路を提案する。

[Vladimir Tepin，ロシア在住]

　正弦波発振器の周波数を変えるには、一対の連動可変抵抗器を用いて、全可変範囲にわたって発振器の平衡条件を満たすように、特性を完全にマッチングさせなければならない。この制約により調整範囲が制限され、コストも高くなり、その結果応用が限られてしまう。

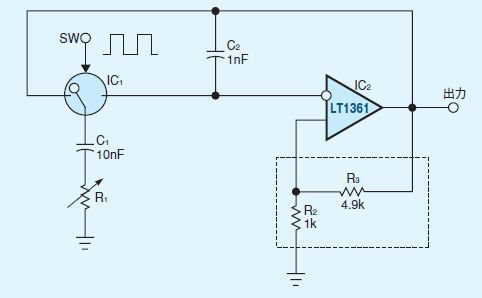
　そのような問題点を解決した正弦波発振器が、図1に示す回路である。1個の可変抵抗器R₁を用いることにより、広範囲の周波数を調整できる。この発振器は平衡条件を満たす必要がないため、マッチングの問題は一切生じない。また、可変抵抗器を接地することは、多くのアプリケーションにとって有利なことでもある。

図1　1個の可変抵抗器で周波数調整が可能な発振器
この正弦波発振器では、出力周波数は接地する抵抗R₁の値にのみ依存する。

　一般的な正弦波RC発振器と同様に、この回路は1個のオペアンプIC₂と2つの帰還ループによって構成されている。1つのループは周波数に依存しない正帰還ループで、2個の固定抵抗（R₂、R₃）を用いている。もう1つのループは周波数に依存する。このループは、コンデンサC₁およびC₂、可変抵抗器R1および単極双投アナログスイッチIC₁を用いており、IC₁はSW入力に印加される周期的な矩形波パルス信号によって駆動される。

　スイッチング周波数FS＝1/Tが発振周波数よりはるかに高く、パルス幅τがスイッチング周期の半分（τ=0.5T）と仮定すると、周波数に依存する帰還ループの電圧伝達関数は、近似的に次式で与えられる。

　ここで発振周波数ω₀＝1/2R√C₁C₂で、d0＝√C₁/C₂＋2√C₂/C₁、そしてd₁＝2√C₂/C₁である。この関数を用いて、正帰還回路の伝達係数をγ＝R₂/（R₂＋R₃）と仮定すると、発振条件として、γ>d₁/d₀＝（2√C₂/C₁）/（2√C₂/C₁＋√C₁/C₂）という関係が得られる。この発振条件はR₁には依存しない。従って、接地している抵抗R₁の制御により、発振周波数のみを制御することができ、発振条件には影響を与えない。つまり、この発振器では広い周波数範囲にわたって、出力の波形を維持しながら、周波数を調整することができる。

　PSpiceシミュレーションの結果、R₁を1.2MΩから1.2kΩまで変化させることにより、発振周波数を3桁（20Hz〜20kHz）にわたって調整できることがわかった。この設計ではIC₂にLT1361を用いており、R2＝1kΩ、R3＝4.9kΩ、C1＝10nF、C2＝1nF、FS＝500kHzとしている。出力電圧振幅は3.2V〜3.3Vである。0kHz〜100kHzの帯域における全高調波歪みは3％を超えない。また、発振周波数は可変抵抗器のコンダクタンス（G₁＝1/R₁）に比例するため、この発振器を広帯域でリニアリティのある「コンダクタンス‐周波数コンバータ」、あるいは「抵抗‐周期コンバータ」としても使える。

Design Ideas〜回路設計アイデア集

【アナログ機能回路】：フィルタ回路や発振回路、センサー回路など

【パワー関連と電源】：ノイズの低減手法、保護回路など

【ディスプレイとドライバ】：LEDの制御、活用法など

【計測とテスト】：簡易テスターの設計例、旧式の計測装置の有効な活用法など

【信号源とパルス処理】：その他のユニークな回路

---

※本記事は、2008年7月29日にEDN Japan臨時増刊として発刊した「珠玉の電気回路200選」に掲載されたものです。著者の所属や社名、部品の品番などは掲載当時の情報ですので、あらかじめご了承ください。
「珠玉の電気回路200選」：EDN Japanの回路アイデア寄稿コラム「Design Ideas」を1冊にまとめたもの。2001〜2008年に掲載された記事の中から200本を厳選し、5つのカテゴリに分けて収録した。