Spiceの新しい応用解析：自然対流問題（その1）：SPICEの仕組みとその活用設計（19）（2/3 ページ）

Spiceが持っている解析能力について基本的な動作とその注意点について説明してきた本連載。今回からは、Spice関連セミナーなどでは、紹介されることの少ない応用解析について説明していきます。

[加藤博二（Sifoen），EDN Japan]

熱抵抗回路網法の課題

　物体（固体）内の熱の流れと温度差は熱抵抗と熱流量で計算できることは前述しましたが、このようにして発熱源から固体の表面まで流れてきた熱は最終的には固体と接している流体（空気）に伝搬・伝導していきます。

　しかし、固体表面〜流体間の熱の移動については、熱の伝導メカニズムが固体内のメカニズムとは異なるため、前出のような簡単な式で熱の流れを求めることはできません。

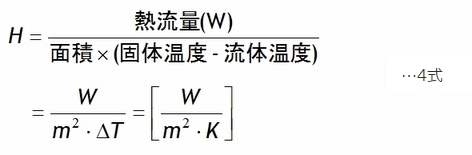
熱伝達係数H

　この固体〜流体間の熱の流れを表す指数として、接触面を通過する熱流量と面の温度差から計算する熱伝達係数Hがあります。計算式を4式に示しますが前出の熱伝導率λと用語が似ていますので混同しないように注意が必要です。

　一般に自然対流問題ではCFDツールを使って流体の熱膨張による比重の変化を浮力にしたブジネスク近似法で流体の運動を解き、得られた熱流量と温度差から4式を用いて熱の流れとしての指数である熱伝達係数Hを算出・表示します。しかしながら、この熱伝達係数Hは熱の流れが求まった上での計算結果であって、物性値ではないということに注意が必要です。

　あくまでも熱解析の計算結果として得られる面を通過する熱流量と温度差から求められる指数であって、CFDツールといえどもこの熱伝達係数Hを計算前に知ることはできないということを覚えておいてください。

熱伝達係数Hの算出法

　前述した熱伝達係数Hには流体の運動を表す対流熱伝達係数Hcと、電磁波として空間に拡散する様子を表す放射熱伝達係数Hrの2種類があります。その1つである対流熱伝達係数Hcは次のように実験式を使って近似的に算出することができます。

対流熱伝達係数Hc

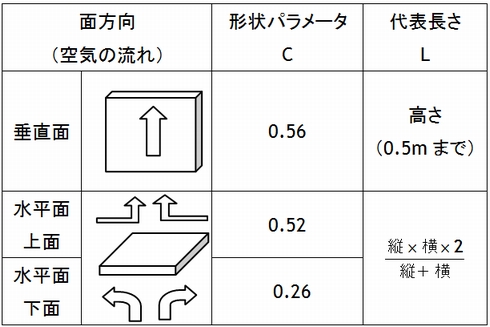
　対流熱伝達係数は対流に起因するものですので重力の影響を受け、物体の面方向によってパラメータが異なってきます。ですから、このパラメータは表2に示す3種類について計算する必要があります。

表2　対流熱伝達係数Hcの形状パラメータ

　対流熱伝達係数Hcの各面共通の基礎計算式を

とまとめれば
C:形状パラメータ/L：代表長さは表2のようになります。

　なお、ΔTは固体と流体（空気）間の温度差であり、この5式や表2が近似的に成立するためには気圧≒1気圧、ΔT＜50Kであり、かつ流体が40〜100℃の空気である必要があります。

　当然、気圧が低下すれば熱を運搬する気体分子が減るわけですからHcは低下し、真空中ではHc＝0になります。（低高度下では△10％/1000mと言われています）

放射熱伝達係数Hr

　放射熱伝達係数Hrは電磁波による熱エネルギーの拡散ですから重力の影響は受けませんし、式中に気圧は含まれませんので真空中でも熱の伝達は可能です。したがって、温度が決まれば各面からの放射強度{W/(m²･K)}は各面で共通になり、シュテファン=ボルツマン則を使って6式で計算できます。

　ここで各定数は次の通りです。

ε:放射係数(0〜1)
σ:シュテファン＝ボルツマン定数(5.67×10⁻⁸)
Tc:固体温度(K)
Ta:周囲温度(K)
ΔT:温度差(Tc-Ta)

　注意する点としてはHrを算出する2点の温度が絶対温度であるという点です。この放射熱伝達による空間への熱拡散は連載17回目の巻末コラムで紹介した空間へのエネルギの散逸量に該当します。

　また、これらの熱伝達係数Hc、Hrにはメッシュに相当するパラメータがありませんので当然ながらメッシュ依存性はありません。

　うれしいことに誰が行っても結果は同じなのです。この点はCFDツールに対して大きなメリットと言えるでしょう。