Spiceの新しい応用解析：自然対流問題（その1）：SPICEの仕組みとその活用設計（19）（3/3 ページ）

Spiceが持っている解析能力について基本的な動作とその注意点について説明してきた本連載。今回からは、Spice関連セミナーなどでは、紹介されることの少ない応用解析について説明していきます。

[加藤博二（Sifoen），EDN Japan]

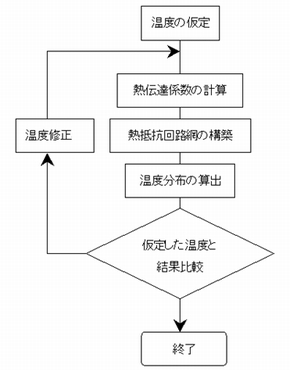
熱抵抗回路網法の計算手順

　熱伝達係数はあらかじめ決めることはできないと書きましたが、前出の熱伝達係数の5式、6式を見ると固体温度Tcと周囲温度Taが分れば熱伝達係数HcやHrは計算で求めることができることが分ります。

　つまり、放射係数ε、周囲温度Taは解析設定条件として既に分かっていますので固体温度Tcを適切な温度に仮定してやれば熱伝達係数は計算できるということです。

　もし、仮定した温度Tcと、それに基づいて計算して得られた固体温度が一致していれば、仮定した固体温度が正しかったことになり、計算は終了します。

　一致していなければ仮定した温度が正しくなかったので、一致するまで収束計算を行えば良いことになります。計算の流れを図2に示します。

図2　熱抵抗回路網の概要【計算の流れ】

Spiceでの計算手順の検討

　VBAマクロなどを使って自分でプログラムを組む場合は図2の計算の実行はそれほど難しいことではありません。

　ただ、今回は回路解析の途中で得られた損失（熱）を検討しようとするものですから、できればツールを切り替えることは避けたいと思います。

　ましてや、開発段階でのヒートシンクの形状算出のためにCFDツールで数十分も計算時間を取られるのは、開発アイデアが途絶えてしまいますので本末転倒です。何とかしてSpiceで熱解析を実行することを考えてみたいと思います。

　まず、熱伝達係数Hの単位について考えます。

　もともと、熱伝達係数は前出のように（W/m²･K）の単位を持っています。従って、これの逆数を取って、面積で割ってやれば熱抵抗の単位を持つ値が得られます。

　具体的には、対流熱伝達係数Hcによる熱抵抗をRth(c)、放射熱伝達係数Hrによる熱抵抗をRth(r)、対象面積をSとすれば

で熱抵抗を求めることができます。

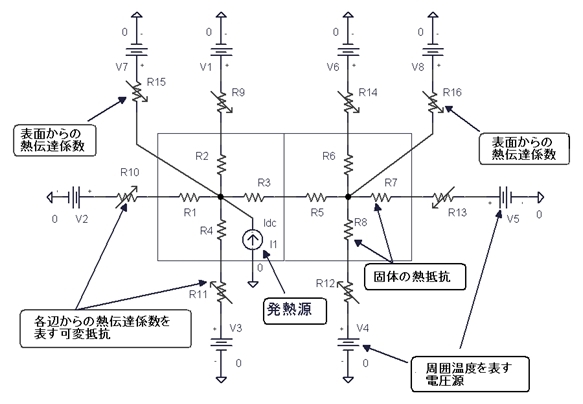
　これらを表面から空気への熱抵抗として電圧依存型抵抗(VR)を使って回路を構築すればバイアスポイント解析で各部の電圧（＝温度）が求められそうです。

　Rth(c)、Rth(r)はTc、Taを表す電圧で制御することになり、イメージ回路図は図3のようになります。しかし、実際に実行してみると、この回路構成ではほとんどの場合、実行できません。

図3　熱抵抗回路網の概要【イメージ回路図】

エラーの原因

　これは回路構成や計算ループの問題ではなく、Spiceの解法アルゴリズムの問題なのです。

　これまで述べてきたように、Spiceは既知のコンダクタンス行列と既知の電流ベクトルに基づいて各部の電圧を求めますが、抵抗値はコンダクタンス行列の構成要素ですので変数で記述することはできません。正しく言うと、変数でも構いませんが、行列演算の時には値が決っていないと解けないのです。

　したがって、抵抗値＝｛電圧÷電流｝という値の与え方をした時、演算結果を持ってきて定数を決めるという矛盾を起し、エラーになって止まってしまうのです。Spiceでの電圧制御抵抗は解に依存しない独立電圧でないと動作しないのが基本なのです。

　では、このような自己矛盾をはらんだ問題についてどのように考えれば良いのでしょうか？

　この問題については次回以降に検討を進めていきたいと思います。

---

参考資料1：CAE懇話会講演資料 07/09/05　第11回中部CAE懇話会資料　｢CFDによる自然対流のカンどころ｣

---

執筆者プロフィール

加藤　博二（かとう　ひろじ）

1951年生まれ。1972年に松下電器産業（現パナソニック）に入社し、電子部品の市場品質担当を経た後、電源装置の開発・設計業務を担当。1979年からSPICEを独力で習得し、後日その経験を生かして、SPICE、有限要素法、熱流体解析ツールなどの数値解析ツールを活用した電源装置の設計手法の開発・導入に従事した。現在は、CAEコンサルタントSifoenのプロジェクト代表として、NPO法人「CAE懇話会」の解析塾のSPICEコースを担当するとともに、Webサイト「Sifoen」において、在職中の経験を基に、電子部品の構造とその使用方法、SPICE用モデルのモデリング手法、電源装置の設計手法、熱設計入門、有限要素法のキーポイントなどを、“分かって設計する”シリーズとして公開している。