漏れインダクタンスを使用したフライバックコンバーター（3） 小信号モデル化：電源設計（3/6 ページ）

この連載の最終回にあたる第3回では、電圧モードで動作し漏れインダクタンスの影響を受けるCCMフライバックコンバーターの小信号応答について検討します。第2回で紹介した更新後の大信号モデルから、最も簡潔なリニアバージョンを確立する目標に向けてステップ形式で作業を進め、徐々に簡略化した小信号回路図を導き出します。この最終的な回路に基づいて、制御側から出力側への伝達関数を抽出し、漏れインダクタンスが伝達関数の分母である品質係数にどのような影響を及ぼすかを示します。

[Christophe Basso（ON Semiconductor France SAS），EDN]

回路図の簡略化

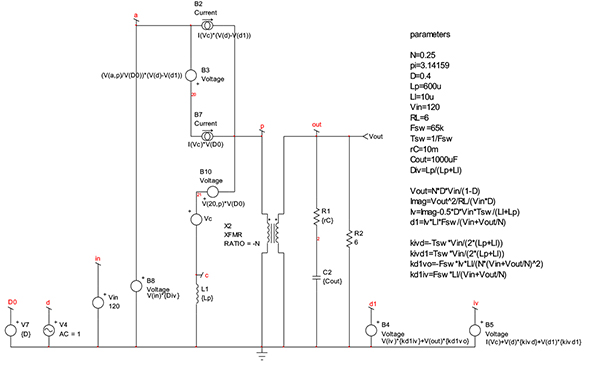
　この回路図から線形化したコンバーターの解析を開始することもできます。さらに簡略化と整理を進めることも可能です。例えば、制御側から出力側への伝達関数で入力電圧V_inは定数です。すなわち、v^{^}_inつまりV_in(s)は0に等しくなります。このように、入力電圧に接続されるノード「a」は、都合よくグランドに接続できます。ノード「a」をグランドに接続すると、回路を再描画して、より簡潔なバージョン（図5参照）を明らかにできます。この回路の周波数応答を図3の周波数応答と比較してテストし、新しく整理したモデルに存在する誤りを検出します。

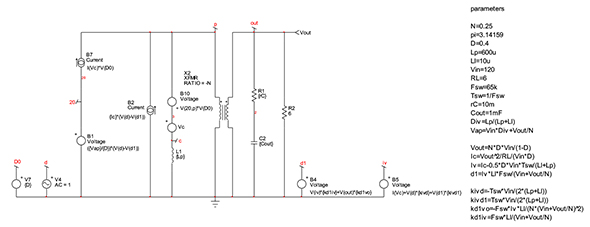
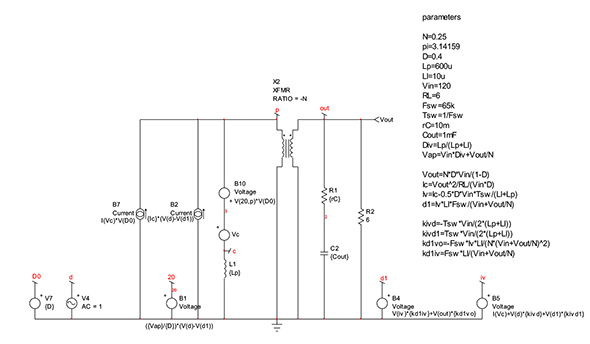
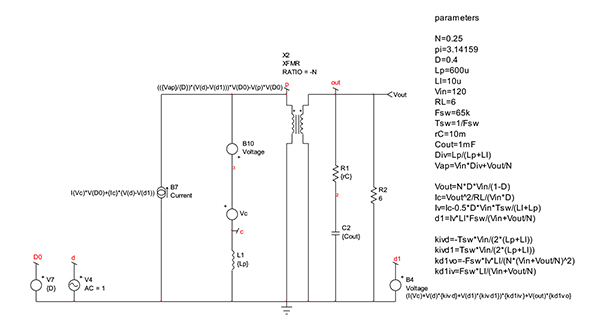
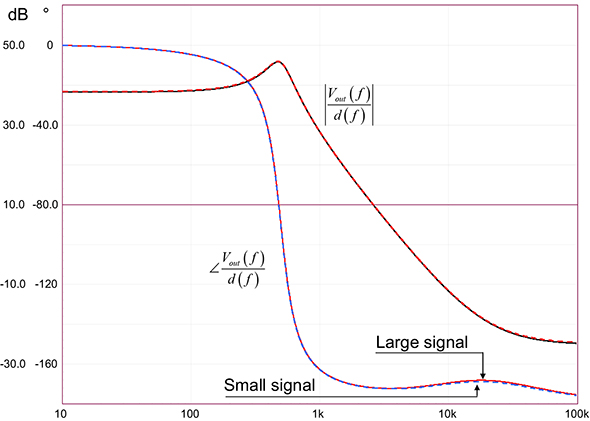
　電流源B₇は電圧源B₁に対して直列です。さらに簡略化を進めるために、B₇の負端子をグランド基準に変換する一方で、B₁は出力をノード20に接続した個別信号源に変換します。新しい回路を図6に示します。ノード20をB₁₀信号源（自らの定義によって更新される）で使用し、両方の電流源B₇/B₂を並列化して単一電流源を形成できます。その結果は図7に示す通りであり、これが解析対象となる最終回路です。信号源I_vを表す式が、d₁信号源に既に含まれていることに注意してください。この回路の周波数応答を、大信号参照モデルの周波数応答と比較する形で作成したプロットを図8に示します。位相応答と振幅応答が同一なので、この最終的な表現について作業を進められます。

図4：更新後の回路に線形化した信号源のみが含まれる

図5：入力電圧が一定であることを考慮すると、ノード「a」をグランドに接続し、小信号回路をさらに簡略化できる

図6：電流源B₇はグランドに接続され、B₁はノード20で自身の電圧を供給

図7：複数の電流源を並列化してB₇を形成し、ノード20をB₁₀に統合することにより、最終的な小信号回路図が得られる。I_vは既にd₁に包含されている

図8：大信号モデルの周波数応答と、図7に示す簡略化した回路の周波数応答は同一