オペアンプのダイナミック応答の検討(1) タイプ2補償回路の使用時:アナログ回路設計(2/6 ページ)
補償回路は、理想的な特性を想定したオペアンプを中心に構築したアクティブ回路が使用されます。ですが、理想的なオペアンプを想定した計算は成立せず、最終的にゲインと位相の深刻な歪みを招く結果になります。開ループゲインと、低周波および高周波にある2つの極が全体的な応答の形状をどのように規定するかが明らかになると、適切なオペアンプを選択できます。
高速分析手法の簡単な紹介
このフィルターのダイナミック応答を決定するのに多数の手法が存在します。この資料では、参考資料[2]と[3]で説明されているFACT(Fast Analytical Circuits Techniques:回路の高速分析手法)を使用します。これらのFACTの背後にある基本的な理論は、励起信号が消滅したとき(Voutが0Vに現象)と応答がゼロになったとき(VFB=0)の2つの異なる条件で回路の時定数を決定することです。この手法を使用して、特定の伝達関数を決定する上でこの手法がどれほど高速で直感的かを確認できます。
参考資料に掲載されているように、ゼロではない擬似静的ゲインを特長とする1次システムの伝達関数は、次の形式で表現できます。
主要項G0は、s=0のときにシステムが示すゲインです。この項が単位を持つ場合は、その単位が式の結果でも使用されます。ここでは、[V]/[V]で表現されるゲインについて説明しているので、単位は使用しておらず、Gは次元のない無名数になります。分子N(s)は伝達関数のうちゼロを表します。数学的にはゼロは応答がゼロになる特定の点を表します。理論的な観点、また全体のs平面を網羅する(ただし、垂直軸は高調波モードでのみ考慮しここでは扱わない)励起信号を考慮する場合は、ゼロの角周波数szが得られるように入力信号をチューニングした時に、出力応答がゼロになるとゼロが自動的に発生します。回路ブロック内で特定のインピーダンスを組み合わせた場合、励起源の存在にかかわらず、信号の伝播と応答は0Vになります。ゼロは分子の根です。これは簡易な数学的抽象化であり、何行にもわたる代数式を記述することなく、検討によって複数のゼロを見つける上で非常に役立ちます。このアプローチの詳細は参考資料[4]に掲載されています。
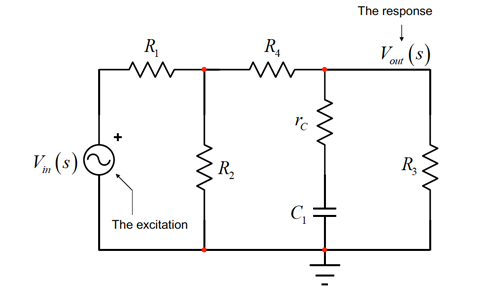
分母D(s)は回路の自然な時定数によって形成されます。これらの時定数τ=RCまたはτ=L/Rは、励起信号をゼロに設定し、この構成で考慮したコンデンサーまたはインダクターから「見た」抵抗を決定することによって得られます。「見る」とは、コンデンサーまたはインダクターを一時的に取り除き、抵抗計をその場所に配置して、表示された抵抗値を読み取ることを意図しています。実際、これは非常に簡単に実施できます。図3を見ると、信号の注入源があります。これは刺激つまり励起であり、回路の左側にバイアス電圧を供給します。入力信号はメッシュとノードを通じて伝播され、抵抗R3の両端で観察される応答を形成します。
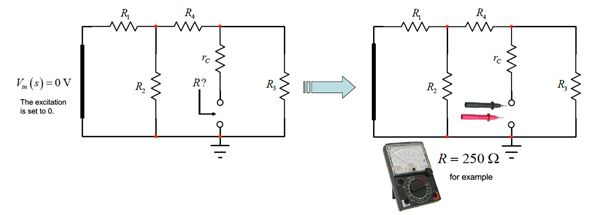
例示したこの回路の時定数を決定するには、励起をゼロに設定し(0Vの電圧源は短絡、0Aの電流源は開路で置き換える)、コンデンサーを取り除きます。次に、(頭の中で)抵抗計を接続し、コンデンサー端子間の抵抗値を決定します。図4にこれらのステップを示します。
図4で演習を行うと、R4と直列接続されているrCを「見る」ことになります。これらの抵抗はR1とR2への並列接続であり、いずれもR3と並列の関係にあります。この回路の時定数は単にRとC1の積に等しくなります。
1次システムの極はそのシステムの時定数の逆数であると示すことができます。したがって、次のようになります。
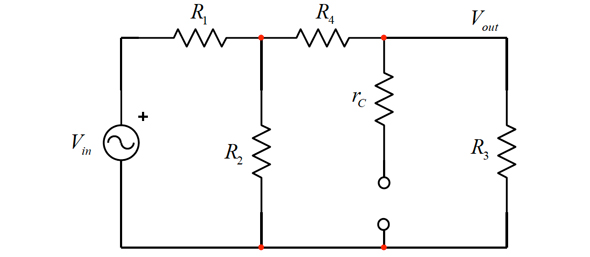
ここで、s=0の時この回路の擬似静止ゲインはいくらでしょうか。DC条件では、コンデンサーは開路になりインダクターは短絡になります。この概念を図3の回路に適用して回路を描き直すと図5が得られます。頭の中で、R4より手前で接続を切断すると、R1とR2で形成された抵抗分割回路が得られます。R2の両端の印加電圧は次の式で表現できます。
出力抵抗RthはR2に並列接続されたR1です。したがって、全体の伝達関数には、R4と直列接続されたRthで構成される抵抗分割回路が関係しており、R3が負荷になります。このDC分析ではコンデンサーC1を取り除くので、rCは図にありません。したがって、次の式が得られます。
Copyright © ITmedia, Inc. All Rights Reserved.