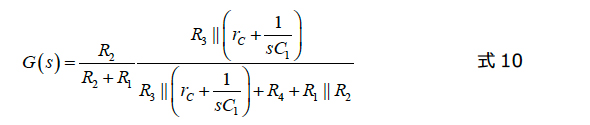オペアンプのダイナミック応答の検討（1） タイプ2補償回路の使用時：アナログ回路設計（3/6 ページ）

補償回路は、理想的な特性を想定したオペアンプを中心に構築したアクティブ回路が使用されます。ですが、理想的なオペアンプを想定した計算は成立せず、最終的にゲインと位相の深刻な歪みを招く結果になります。開ループゲインと、低周波および高周波にある2つの極が全体的な応答の形状をどのように規定するかが明らかになると、適切なオペアンプを選択できます。

[Christophe Basso（ON Semiconductor France SAS），EDN]

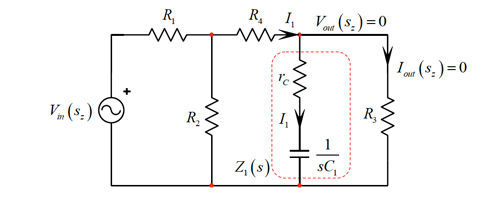
　これで分析はほぼ終わりですがゼロが存在していません。仮にゼロが存在する場合、それをどのように把握すればよいでしょうか。この場合、役に立つ対処方法があります。図3の回路を考え、頭の中でコンデンサーC₁の両端を短絡します。ここで、短絡したコンデンサーを含む回路に電圧を印加すると想定します。つまり、オシロスコープでV_outの応答を観察できるでしょうか。確かに、r_CがR₃を短絡し、おそらく振幅は小さくなるでしょうが、入力信号は引き続き伝達され応答が存在します。この設問に対する回答が「はい、C₁を短絡しても応答があります」の場合、C₁に関連付けられたゼロが存在します。インダクターL₁が存在する回路を扱う場合、同じ演習を実施しますが、今度はインダクターを開路として扱います。このモードで応答がある場合、L₁に関係するゼロが存在します。

　前述した通り、励起信号の伝達を阻止するとゼロが自動的に発生し、この時、出力はゼロになります。今度は変形した回路を検討します。ここでは、図6に示すようにC₁を1/sC₁で置き換えます。応答がゼロになる特定の条件とは、どのようなものでしょうか。応答がゼロになることは単純にはR₃を流れる電流がゼロになることです。抵抗に電流が流れていない場合、その抵抗の両端に電圧は印加されず、V_outは0Vになります。

図6：この変形後の回路で、r_CとC₁の直列接続が実質上の短絡となる場合、応答は消失する （クリックで拡大）

　R₃に電流が流れない場合、r_Cと1/sC₁の直列接続により実質上の短絡が形成されます。

　この場合の根s_zが求めようとしているゼロ位置です。

　次のように変形できます。

　これら全ての結果をまとめると、図3の回路の特性を表す最終的な伝達関数が得られます。

　これを「低エントロピー」の式と呼んでいますが、この中でゲイン、1つの極、1つのゼロを簡単に区別できます。一方、「高エントロピー」の式は、例えばインピーダンス分割回路を検討すると、元の回路に対して総当たり法を適用して、次の式を求めることができます。

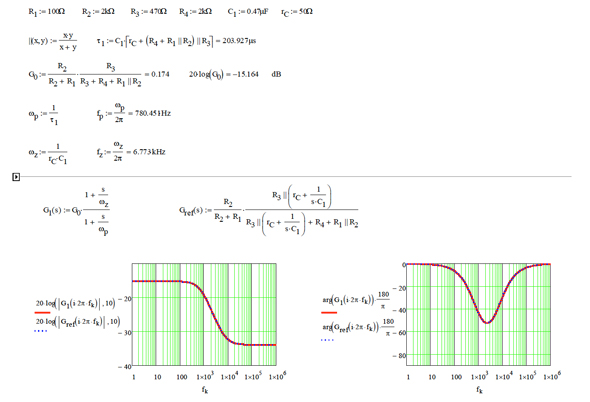
　ただし、このような式を導くときにミスをする可能性があります。実際、筆者はミスをしていました。加えて、式9のように変形するにはかなり手間がかかります。また、式9を記述する際に、最初から1行の代数式で表現したわけではないことに注意してください。後からミスに気付いた場合は、個別の回路図に戻って、個々にミスを修正すれば容易に対処できます。そうすると、式9の修正も簡単になります。ここで、式10でも同じく修正してみますが、おそらく最初からやり直すことになるでしょう。図7に示すように、Mathcadシートで周波数応答をプロットして、式9と式10が同じかどうかをチェックできます。

図7：Mathcadを実行すると、FACTを使用して導いた式が、未加工の式が示す応答に一致するかどうかを確認できる

　以上、手短にFACTを紹介したのは、回路が簡単でも複雑でも、この手法がどれほど快適で効率的であるかを示すためです。複雑なアーキテクチャをシンプルな個別回路に分割すると、上記のように素早く伝達関数を導くことができます。これでツールを紹介したので、タイプ2の補償回路に適用してみましょう。