オペアンプのダイナミック応答の検討(1) タイプ2補償回路の使用時:アナログ回路設計(4/6 ページ)
補償回路は、理想的な特性を想定したオペアンプを中心に構築したアクティブ回路が使用されます。ですが、理想的なオペアンプを想定した計算は成立せず、最終的にゲインと位相の深刻な歪みを招く結果になります。開ループゲインと、低周波および高周波にある2つの極が全体的な応答の形状をどのように規定するかが明らかになると、適切なオペアンプを選択できます。
FACTをタイプ2の補償回路に適用
FACTを効率的に図2の回路に適用するために、最初にエネルギー蓄積素子C1とC2を検討します。それぞれの独立状態変数を検討します。つまり、互いに直列接続も並列接続もされていない状態で、これは2次システムに相当します。このようなシステムは、擬似静止ゲインがゼロでないと仮定して、次の形式で表現できます。
2次システムの場合、分母が次の式に従うことを示すことができます。
sに対応する係数は単純に、励起をゼロにして決定した複数の時定数の和に等しくなります。s2に対応する係数は、新しい表現τ12を導入するため多少複雑になります。この表現はC1を短絡で置き換えた状態でC2の端子から「見た」抵抗を意味します。一見すると謎めいた説明に思えますが、少し考えてみると解決は可能です。
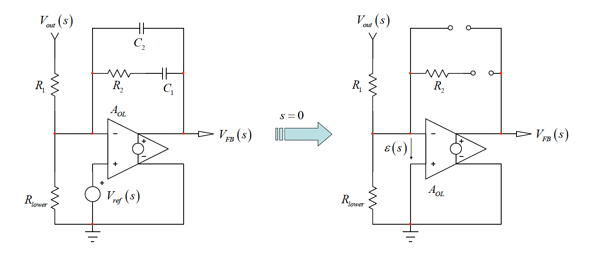
図3の回路を解決するために採用したパスに従うと、s=0に対応するシステムを分析できます。図8にこのパスを示します。分析の際に、Vrefが理想的な電圧源であり、そのダイナミック応答はゼロです(どのような変調を加えても、その電圧は固定電圧である)。このように、コンデンサーは小信号回路から自然に消失し、AC分析では短絡の形をとります。
オペアンプは、εと開ループゲインAOLの積に等しい電圧を出力します。反転入力ピンの電圧には、ローサイド抵抗Rlowerが関係しており、εはこのケースではゼロ以外の値です。
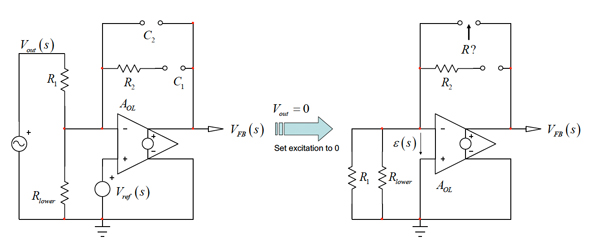
この回路には2個のコンデンサーがあるので、2個の別々の時定数が存在します。C2が関係する最初の時定数を決定するには、励起信号をゼロに設定し、C1を回路から取り除いた状態でC2の端子から見た抵抗を決定します。変形の過程を図9に示します。
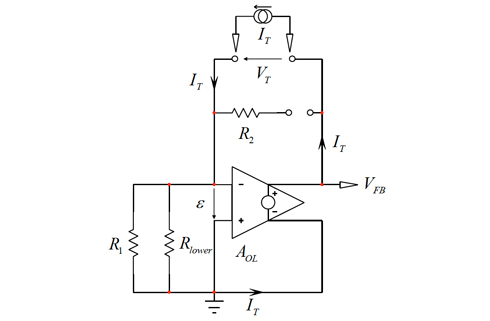
最初の例で検討方法が十分に機能していた場合、今回は電圧制御の信号源(つまりオペアンプ)が存在するので簡単なアプローチとはなりません。C2の両端でみられる抵抗を決定するために、テスト用電流生成源ITを接続できます。それにより、端子間に印加される電圧を決定できます。VT/ITを計算すると、求めようとしている抵抗値が得られます。電流源が存在する回路を図10に示します。記述できる最初の簡単な式にはが関係します。オペアンプの入力ピン間の電圧は、R1とRlowerの並列合成抵抗にかかる負電圧です。
オペアンプの出力は、に開ループゲインAOLを乗算した値になります。したがって、
式14を式15に代入すると、次の式が得られます。
VTは電流源に印加される電圧です。左側の端子にはマイナスのεが存在し、右側にはバイアスVFBが印加されます。電位差は次のようになります。
式17からVFBを取り出すと式16の結果に等しいので、整理して次の式が得られます。
抵抗は単純に次の式で表せます。
したがって、最初の時定数τ2は、次の式で表せます。
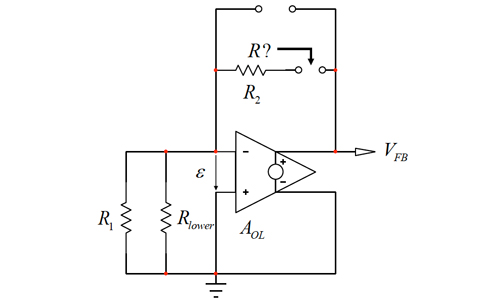
C1が関係する2番目の時定数を求めるには、図11に示す更新された回路図が必要です。結果は明白なので今回は電流生成源を取り付けません。C1の端子間でみられる抵抗は、R2を直列接続した場合のC2に対して既に決定されています。
Copyright © ITmedia, Inc. All Rights Reserved.