電磁気学入門（4）コアレス〜相互インダクタンス損失と渦電流損失： DC-DCコンバーター活用講座（47）（2/2 ページ）

電磁気学入門講座。今回は「相互インダクタンス損失」と「渦電流損失」について説明していきます。

[Steve Roberts（RECOM），EDN Japan]

渦電流損失

　全ての磁性体コアは電気伝導性で、レンツの法則（誘導電流が流れる場合、その方向は常に変化の逆になる）により、いかなるコア内の磁界の変化は、磁束の変化と逆に流れる電流（渦電流）を誘導します。

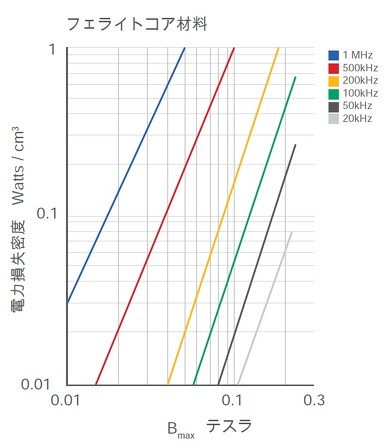
　渦電流の影響は、コアへの磁束透過の制限、そしてコアでの電力損失があり、両方ともに望まれるものではありません。渦電流による電力損失はi²（t）Rに等しく、電力損失は磁界励磁周波数の二乗で増加します。全体の損失概算は、シュタインメッツの式で求められます。

式3：渦電流による電力損失

　K_Eはコア材料による係数（例：鉄、鉄粉、フェライトなど）、fは磁束変化の周波数、Bは最大磁界強度、V_coreはコアの実効体積です。周波数が一定の場合、コア材料cm³あたりの渦電流電力損失の二乗は、磁束の二乗に線形依存します。

　周波数、コア材料、最大磁束は主に他の設計要因により決まるので、渦電流損失はコアの実効サイズの削減のみにより低減することができ、薄い金属シートによる積層コア、または小さな粒子の焼結磁性材料による鉄粉またはフェライトコアが選択肢になります。

図2：シュタインメッツの式によるフェライトコア材料の全電力損失

実用的ヒント

　実際のところ、シュタインメッツの式による損失の関係は完全に直線ではありませんが、式としての浅い曲線は、精度を損なう前の初期開始点から離して引き延ばすことはできません。この誤差は、信号のデューティサイクルと波形にも依存しますが（シュタインメッツの式は正弦波の磁束変化を想定）、初期の概算としては、この式は予期されるコア損失を計算するための便利なツールです。

図3：等価渦電流図式

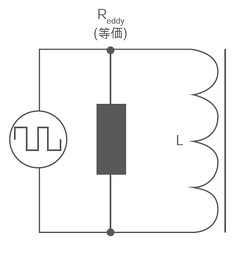
　渦電流損失に関する他の考え方としては、コアのインダクタンスと並列な抵抗と仮定することができます。

　抵抗で消費する電力は、与えられた電圧の二乗になります。しかしながら、巻き線（および並列の等価渦電流抵抗R_eddy）の電圧はPWM変調されているので、平均電力損失はデューティサイクルδに依存します。動作周波数が一定の場合の渦電流損失は以下の式で表せます。

式4：渦電流損失

　PWMによる安定化では、入力電圧が倍になるとデューティサイクルを半分にして、コアの磁束振幅を同じに維持します。しかしながら、渦電流の損失の合計は、V_in²の係数により、倍のままです。この問題の解決策は、電圧に伴って周波数を変更することで、入力電圧が倍になった場合には周波数を半分にします。これで、渦電流損失は、入力電圧の変化に対して安定して変わりません。ただ、周波数が変動すると、効率やEMIといった他の問題を引き起こす可能性があり、最終的な決定には妥協が必要です。

⇒次の記事を読む

⇒「DC-DCコンバーター活用講座」連載バックナンバーはこちら

執筆者プロフィール

Steve Roberts

英国生まれ。ロンドンのブルネル大学（現在はウエスト・ロンドン大学）で物理・電子工学の学士（理学）号を取得後、University College Hospitalに勤務。その後、科学博物館で12年間インタラクティブ部門担当主任として勤務する間に、University College Londonで修士（理学）号を取得。オーストリアに渡って、RECOMのテクニカル・サポート・チームに加わり、カスタム・コンバーターの開発とお客様対応を担当。その後、オーストリア、グムンデンの新本社で、RECOM Groupのテクニカル・ディレクタに就任。

---

※本連載は、RECOMが発行した「DC/DC知識の本　ユーザーのための実用的ヒント」（2014年）を転載しています。