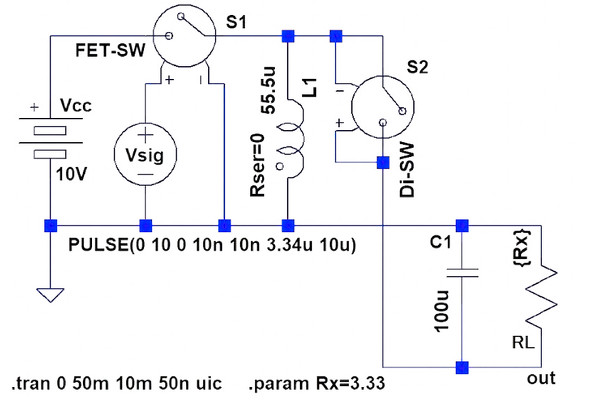
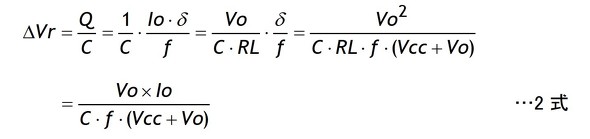反転形DC/DCコンバーターの設計(5)連続モードのリップル電圧計算:たった2つの式で始めるDC/DCコンバーターの設計(19)(1/3 ページ)
今回はチョーク電流連続でキャパシターへの充電期間tcがtc=toffとなるMode I動作時のリップル電圧とキャパシターに流れるリップル電流の計算の仕方について説明していきます。
前回はリップル電圧を取り上げる予定でしたが説明の流れからチョーク電流が不連続になった時のコンバーターの挙動を先に説明しました。その中で電流不連続モードではオン時間を制御することで電圧変換比を時比率δで決まる値以上に大きくできることを説明しました。しかし万が一オン時間制御が外れると負荷によっては出力電圧が危険電圧に達することがあること、そしてその危険を防止するため確実に動作する信頼性の高い保護回路が同時に必要になることなどは忘れてはならないチェックポイントといえるでしょう。
今回は前回説明を延期したチョーク電流連続でキャパシターへの充電期間tcがtc=toffとなるMode I*動作時のリップル電圧とキャパシターに流れるリップル電流の計算の仕方について説明していきます。
ここで使用する記号と定義は次の通りです。
ILP:チョーク電流の最大値 L:チョークL1のインダクタンス値 IL:チョーク電流
Iin:入力電流(DC) Vcc:入力電圧 Vo:出力電圧
Io:出力電流(DC) Po:出力電力 RL:負荷抵抗
*)Mode I:チョーク電流は連続でありtoffの全区間で平滑キャパシターを充電するモード
Mode II:チョーク電流は連続だがtoffの一部区間で平滑キャパシターを充電するモード
Mode Iのリップル電圧の図式解法
この章は「2つの式」を離れて図1に示す基本回路図から得られる各部の波形の図式解法でMode Iのリップル電圧を求めていきます。ここでの計算手順は前シリーズのステップアップ型コンバーターと同様に、図1の波形を表現するための1次式使います。
①ton期間(ts×δ)中はFET-SW(S1)がオン、Di-SW(S2)がオフですからチョークL1に磁気エネルギーが蓄積されると同時にキャパシターC1は負荷抵抗RLによって放電し両端電圧Voは減少します。
そして
②toff期間[ts×(1−δ)]中は各スイッチの状態が入れ替わり①でチョークに蓄積された磁気エネルギーによってキャパシターC1は充電され、Voは増加します。
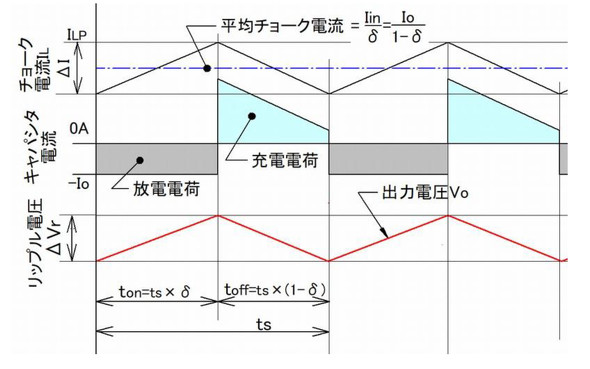
上記の関係を図2に示します。この図において出力電圧Voは負極性なので減少は0Vへの漸近、増加は0Vからの離反を表します。両者とも変化幅自体は微少でありDC成分を超えることはないとします。
回路を流れる電荷Qは同図から分かるように、ton期間中にQ=Io×tonの電荷がキャパシターC1から負荷抵抗RLに供給されΔVrだけキャパシターC1の電圧は減少します。その後、C1が放電した電荷Qは同量がtoff期間中にチョークL1から供給され初期の電圧まで回復(増加)します。
C1を出入りする電荷Qは図2の各着色部の面積に相当します。チョークL1によるC1への充電電流は台形波ですがここでは前シリーズのステップアップ形に倣ってton時の方形波の面積で計算します。電荷Qの定義はQ=i×tですから1式で表せます。
リップル電圧ΔVrは1式の電荷Qを電圧に換算したものです。ですからリップル電圧ΔVrはCの定義式(C=Q/V)に従って2式で計算できます。
2式からリップル電圧ΔVrは出力電流Ioに比例すること、そしてステップアップ形と同様にチョークL1の値には無関係であることが分かります。このLの値は不連続になる臨界電流や後述するキャパシターC1のリップル電流に影響します。
(f×C)が一定であればリップル電圧は同じですから高周波(f大)化すれば小容量の平滑キャパシターで済み小型化の面で有利になります。
Copyright © ITmedia, Inc. All Rights Reserved.