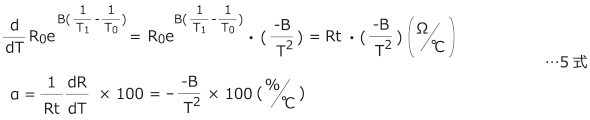サーミスタ(3) ―― NTCサーミスタによる温度検出回路:中堅技術者に贈る電子部品“徹底”活用講座(13)(1/4 ページ)
今回は、NTCサーミスタの基本的な用語解説と、NTCサーミスタの応用回路例としての温度検出回路について説明します。
前回はNTCサーミスタを用いた突入電流制限回路の設計上の注意点について説明しました。
今回はここまで説明の機会がなかった残りのNTCサーミスタの用語と、NTCサーミスタの応用回路例としての温度検出回路について説明したいと思います。
B定数の温度特性
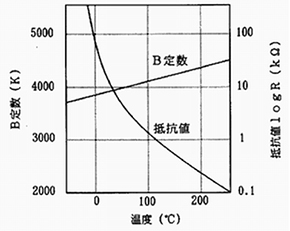
サーミスタ編の連載第1回でNTCサーミスタの温度は1式で表されると述べましたが、実際のサーミスタのB定数は定数ではなく、材料組成によっては参考図に示すように最大5K/℃程度の温度特性を持ちます。したがって広い温度範囲に1式を適用すると、厳密には実測値と差が生じます。
実測との誤差を減らす目的でB定数を2式のような温度Tの2次関数として近似することもしばしば行われます。(a、b、cは係数)
※製造に起因するB定数の変動は2式の係数cの変動となりaやbにあまり影響を与えないと考えられています。
係数a、b、cの算出
係数a、b、cは2次関数の係数として定義されていますが3個の係数を完全に決定するには3つのB値が必要なので(T0,R0)、(T1,R1)、(T2,T2)、(T3,R4)の4つの測定点が必要になります。
- 最初に各区間のB定数を求めます。(温度T0基準)
- B1〜B3の値が決まれば4式を解いて係数a、b、cを求めることができます。
これらを踏まえるとNTCサーミスタの特性例は参考図に示すようになります。また、この他にも、特性項目としては熱放散定数、熱時定数、温度低減率などがあります。
抵抗温度係数
任意の温度での1℃当りのゼロ負荷抵抗の変化率を表す係数を抵抗温度係数(α)と言います。
この抵抗温度係数(α)とB値との関係は、1式を微分した5式で計算できます。
αに負の符号がついていますので温度が上がるとゼロ負荷抵抗は減少し、分母にT2項がありますので変化率自体は温度上昇とともに0に漸近します。
Copyright © ITmedia, Inc. All Rights Reserved.