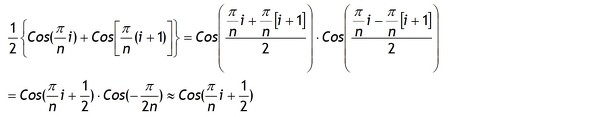ジャンクション温度の計算(4)―― 正弦波形損失の温度計算:中堅技術者に贈る電子部品“徹底”活用講座(78)(2/2 ページ)
今回はここまでの考え方に従って損失変化が直線ではなく正弦波で表される事例について検討を進めます。
数値計算による解法
この8式をJについて微分し0と置けばピーク温度に達するステップ時間を求めることができるのですがこの式を微分することすら簡単ではありません。ですので本稿では数値的に7式を計算することにします。ここではこの計算手法を1次の前進法と呼ぶことにします。
なおピーク温度に達するステップ数Jは数値計算の恒(つね)として計算区切りによって1ステップ前後しますのでnが小さい領域では影響が大きく曲線が波打ちます。この対策としてピーク値を含む前後の測定値を用いてスムージング処理を施しています。
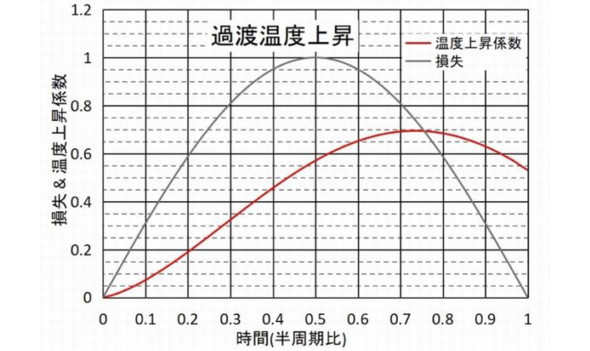
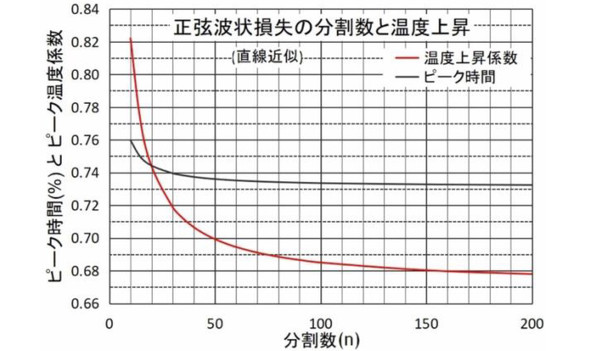
図3は温度上昇のイメージをつかむためにある分割数で温度上昇の様子を表した図であり、図4は7式の分割数nと区間でのピーク温度を示した時の温度上昇係数および、ピーク時間の変化をグラフにしたものです。
図4の結果から計算結果の収束速度が遅く、温度上昇係数が+10%の誤差に収まる時の分割数は20分割(+10.8%)以上が必要になります(中点法n=200分割を基準とした場合)。
単純な増加形三角形の例では誤差10%以下になる分割数は10分割以下でした。このように誤差率が低減せず収束が遅いのは三角形損失では損失増加率が一定であったのに対して正弦波損失では損失増加率も時間変化し、誤差因子として影響するためと考えられます。
中点法の導入
ここまでは三角形損失の場合と比較すると共に積分のしやすさや級数の扱いやすさの観点から数値計算でいう1次近似の前進法の考え方に基づいて計算を進めてきました。
しかし正弦波損失の例のように誤差項が複数項にわたって組み入れられると収束や精度の点で欠点が目立ってきます。
ここでは改善策として2次の前進法でありながら比較的扱いが簡便な中点法の考え方を使った事例を紹介します。
中点法は簡単に言うと現時点と次時点の中間時点の傾きを使って計算します。
現時点と次時点、それぞれの傾きを使う2次の陰的解法の代表は台形法ですが中点法は1/2ステップ進んだ時点の1つの傾きだけを使うので計算は簡単になります。
[台形法との比較]
前述したように損失の変化分ΔPは次のようになります。ここでΔi=1です。
台形法ではステップiの損失増加分ΔPiとステップ(i+1)の損失増加分ΔPi+1の平均値を使用しますのでそれぞれを求めます。簡略化のため余弦項のみを記します。
ここで
です。
このように今回の正弦波損失の例では台形法は時間刻みを0.5ステップ進めた時点の損失増加分使った中点法と効果と同じということになります。つまり、この事例では中点法は陰解法と陽解法の違いがありますが台形法と同等の2次精度であることが期待できます。
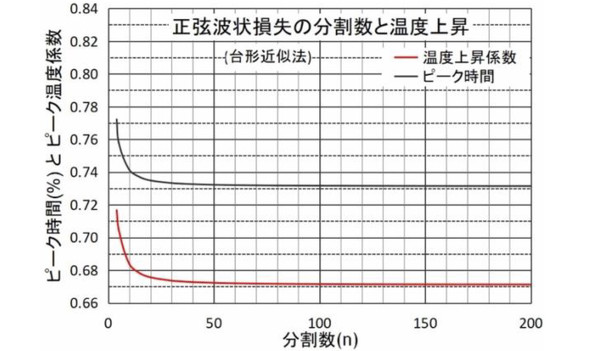
中点法を用いてn=200までの計算結果をまとめたものが図5です。中点法ではn=100以上の分割で計算結果は収束し、図4の結果と比べて改善されていることが分かります。この結果から求める最終の結果は、
ピーク温度係数 =0.671235459
ピーク時間 =0.731410513
程度と分かり、誤差10%程度を許容するのであれば4分割の中点法で0.717(+6.8%)が得られています。
(前進法では30〜40分割で0.719〜0.707)
また図4(従来法)のn=50とn=100の同値になる中点法の分割数nを比較したものが表1です。2次近似の精度はn2に比例すると言われていますが1次近似と比較すると√(n)の分割数で1次近似と同等な予測値が得られることが確認できます。ただしピーク時間は2次補正を行ったとは言え2次補正は温度係数の補正が主ですから分割数の影響が強く表れているようです。
| 分割数:低 | 分割数:高 | |||
| 中点法(n=5) | 前進法(n=50) | 中点法(n=10) | 前進法(n=100) | |
| ピーク温度係数 | 0.705(+5.1%) | 0.699(+4.2%) | 0.684(+1.9%) | 0.685(+2.0%) |
| ピーク時間 | 0.758(+3.7%) | 0.736(+0.7%) | 0.741(+1.4%) | 0.734(+0.4%) |
| 表1:解析結果の比較* *表1において()は中点法n=200の値を基準にした時の偏差です。 | ||||
ここまでは単パルス損失が発生した時の温度上昇の求め方について説明してきました。最終的には実機の温度上昇を求めたいのですが実機では単パルスではなく繰り返し損失が発生します。次回はこの繰り返し損失波形の温度上昇について考えていきます。
執筆者プロフィール
加藤 博二(かとう ひろじ)
1951年生まれ。1972年に松下電器産業(現パナソニック)に入社し、電子部品の市場品質担当を経た後、電源装置の開発・設計業務を担当。1979年からSPICEを独力で習得し、後日その経験を生かして、SPICE、有限要素法、熱流体解析ツールなどの数値解析ツールを活用した電源装置の設計手法の開発・導入に従事した。現在は、CAEコンサルタントSifoenのプロジェクト代表として、NPO法人「CAE懇話会」の解析塾のSPICEコースを担当するとともに、Webサイト「Sifoen」において、在職中の経験を基に、電子部品の構造とその使用方法、SPICE用モデルのモデリング手法、電源装置の設計手法、熱設計入門、有限要素法のキーポイントなどを、“分かって設計する”シリーズとして公開している。
Copyright © ITmedia, Inc. All Rights Reserved.
関連記事
 ワイヤーボンド(4) ―― 銅ワイヤーの評価項目とその注意点
ワイヤーボンド(4) ―― 銅ワイヤーの評価項目とその注意点
今回はコストダウンの一環として導入が進められている銅ワイヤーの評価項目とその注意点について説明します。 ワイヤーボンド(3) ―― ワイヤーボンドの評価法
ワイヤーボンド(3) ―― ワイヤーボンドの評価法
今回は銅ワイヤーについて説明する予定でしたが、その一環としてワイヤーボンドの評価法について説明します。 ワイヤーボンド(2) ―― 関連用語や治具、不良について
ワイヤーボンド(2) ―― 関連用語や治具、不良について
今回はワイヤーボンドの用語、治具および、ワイヤーボンドの不良について説明します。 ワイヤーボンド(1) ―― ワイヤーボンディングとは
ワイヤーボンド(1) ―― ワイヤーボンディングとは
今回から、半導体チップと外部電極との接続する「ワイヤーボンド」について解説していきます。 半導体(7) ―― MOSFETのゲート駆動回路の注意点(2)
半導体(7) ―― MOSFETのゲート駆動回路の注意点(2)
今回はパワーMOSFETの構造とそれに起因する寄生容量について説明するとともに、引き続きゲート駆動回路を中心にした使い方の注意事項を説明します。前回の記事と併せて読んでいただければ理解も深まると思います。 半導体(1) ―― 半導体の製造工程
半導体(1) ―― 半導体の製造工程
今回からは電子回路に欠かせない半導体について説明します。本シリーズでは半導体の市場不良および、その原因を説明するための製造工程の問題を主眼に説明をしていきます。