デジタルフィルターとアナログフィルター(2)――デジタルフィルターの動きを見ながら理解する:ソリューションライブラリ
信号処理用フィルターについて解説する本連載。今回は、デジタルフィルターに着目し、フィルターにはどのようなものがあってどのような違いがあるのかを紹介しながら、実際にフィルターを動かしてみたいと思います。
ソリューションライブラリ第1回「デジタルフィルターとアナログフィルター(1)――デジタルフィルター超入門編」では、デジタルフィルターとアナログフィルターそれぞれの特長について解説し、それぞれの原理や特性について技術的な視点から紹介しました。
第2回となる今回は「デジタルフィルターとアナログフィルター(2)デジタルフィルターの動きを見ながら理解する」と題して、デジタルフィルターに着目し、フィルターにはどのようなものがあってどのような違いがあるのかを紹介しながら、実際にフィルターを動かしてみたいと思います。
1)移動平均フィルターの問題点
第1回で、フィルターにはFIRフィルターとIIRフィルターがあり、最も簡単なものに移動平均によるフィルター処理があることを紹介しました。
さて、信号処理において移動平均フィルターだけ知っておけばノイズ対策は万全なのでしょうか?
実は、移動平均フィルターには欠点があります。これから実例をご紹介します。
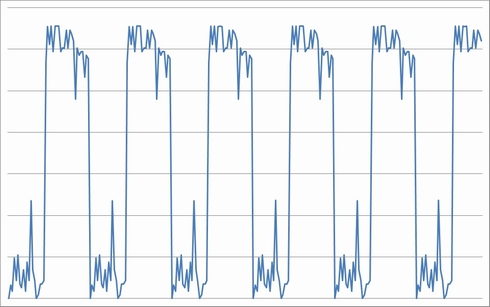
例えば、図1のようなノイズ波形があったとします。
この波形に対して、N=10で移動平均をかけてみましょう。
かなりのノイズが除去できたように見えますが、まだ少しいびつな形が残っています。
では、さらに移動平均を強くかけてみます。次数を増やしてN=20としましょう。
元の形から、だいぶ離れてしまいました。また、N数が増えるほど振幅のピーク値も落ちてきます。
移動平均は、複雑な公式が不要で比較的手軽に使えるのがメリットですが、ノイズ除去を期待して次数を上げていくとこのように、早い段階で波形が崩れてしまい、オリジナルの波形とだいぶ変わってしまいます。そのため移動平均はノイズ対策にベストな手法とはいえません。
2)ノイズを把握する ―フーリエ解析―
そもそも、ノイズ成分というのはどこに潜んでいるのでしょうか。ノイズ対策を行うには、まず「ノイズを知る」ことが重要です。
先にご紹介した図1は、時間軸に伴ってプロットされた波形です。これを周波数軸に伴った波形に変換します。ここではフーリエ変換を用います。
フーリエ変換を使うと、時間軸のデータ郡を周波数軸のデータ群に変換することができます。
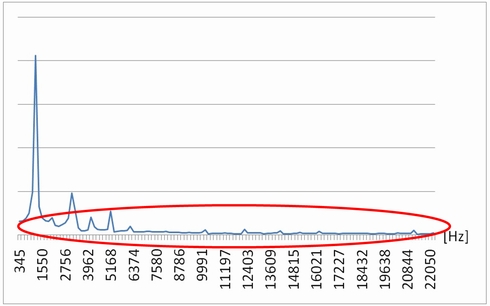
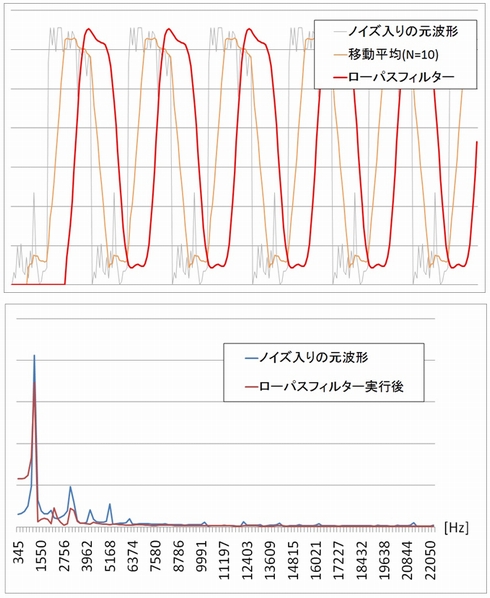
図1の波形に対して、フーリエ変換を実行し、周波数を横軸にとってプロットしたものを図4に示します。
一番レベルの高い周波数成分が必要な波形ですが、それ以外に部分的に飛び出ている箇所がありますね。
これらが必要な信号以外の雑音(ノイズ)と判断します。これらノイズを必要とする波形を壊さずにできるだけ取り除くことができれば良いのです。
3)ローパスフィルターを活用する
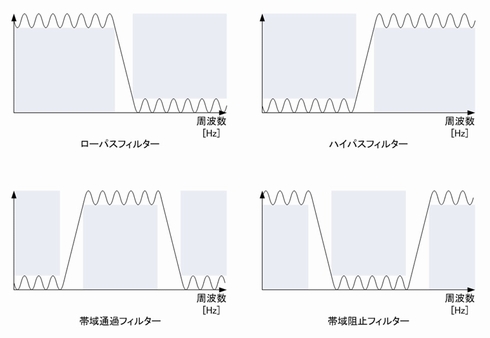
移動平均法によるフィルタリングでは、周波数に関係なく均等に処理が行われます。これだと、残しておきたい周波数成分までつぶしてしまいます。そこで移動平均法に変わって登場するのが、ローパスフィルターです。
ローパスフィルターは、低域の周波数帯はほぼ変えずに中広域の周波数帯を減衰させる特性を持ったフィルターです。図4ではノイズ成分と思われる箇所が3000Hz以降に表れていますので、3000Hz以降を除去するローパスフィルターに通してみます。
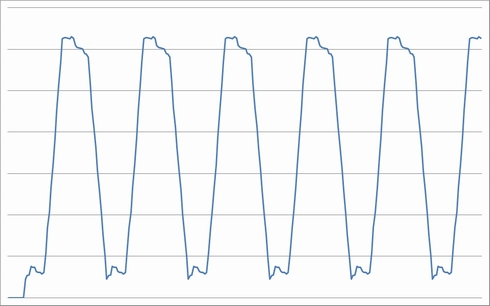
図5がローパスフィルターをかけた結果です。
フーリエ解析してみると、ノイズ成分が減衰しているのが分かります。
今回はローパスフィルターを例に紹介しましたが、他にもローパスフィルターとは逆に、低域の周波数成分を減衰させ、広域を通過させるハイパスフィルターや特定の帯域だけを通過させる帯域通過(バンドパス)フィルターなど用途に応じて幾つか種類があり、実際の組み込みではこれらを使い分けます。
4)FIRフィルターとIIRフィルターの使い分け
ローパスフィルターについてご紹介しましたが、今回はFIRフィルターとIIRフィルターについてです。果たして、両者はどのような特徴があるのでしょうか。
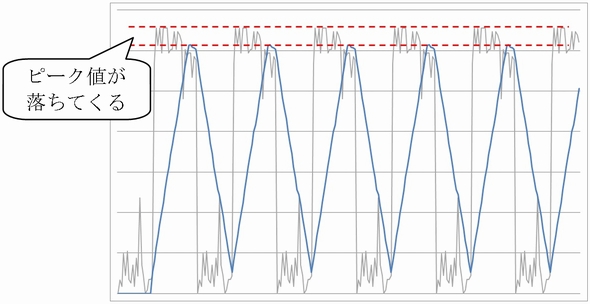
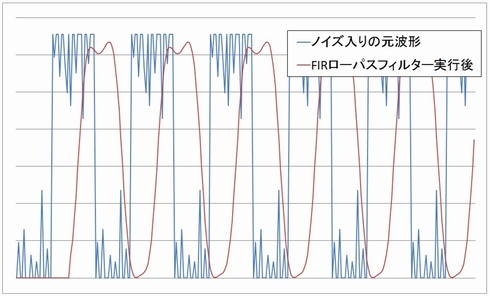
図7にノイズ入りの元波形(青)と、それに対してFIRローパスフィルターをかけた後の波形(赤)を示します。
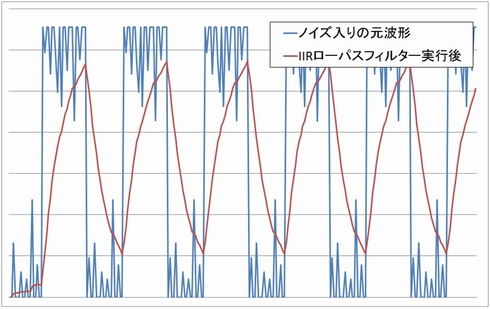
同じように、元波形に対してIIRローパスフィルターをかけたグラフを図8に示します。
IIRローパスフィルターを通した結果はご覧のように元の波形からだいぶ崩れてしまいました。これは、IIRフィルターには直線位相特性を維持できないという特徴を持っていることにあります。
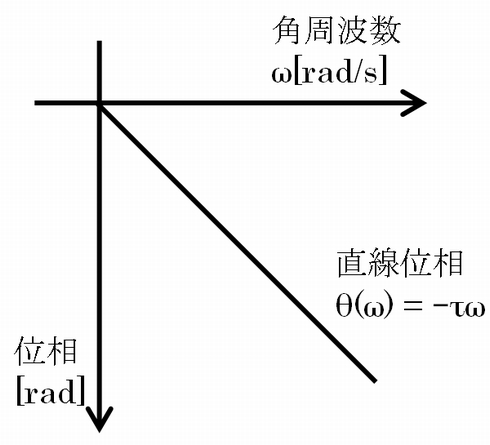
この直線位相特性とは、位相[rad]に対して角周波数ω[rad/s]の関係が、以下のように成り立つことをいます。τは定数で、任意の角周波数に対する遅延時間を意味します。これが一定である場合に直線位相特性(θ(ω)=-τω)があるということになります。
FIRフィルターは直線位相特性を維持できるため、図7のようにノイズ波形に対して有効に働きます。
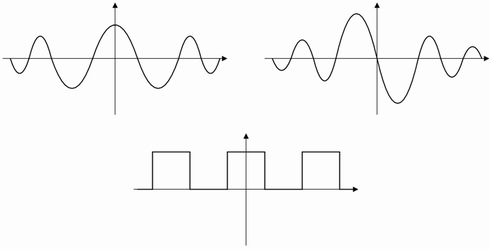
直線位相特性のある波形は図9のような波形になり、対照的なインパルス応答が得られます。
対してIIRフィルターは、直線位相特性を維持できないというマイナス面があるものの、回路規模が小さくできることが最大のメリットです。デジタルフィルターを最終的にハードウェアに置き換えることを考える場合、IIRフィルターによる信号処理の実現を考慮するとよいでしょう。
デジタルフィルターは、場面に応じて使い分けることが重要になります。
5)動きを見てみよう!
デジタルフィルターについて語るには、多くのことを書かなければなりませんが、ここではデジタルフィルターはどういうものかを実際に動かしてみるためのデモファイルを用意しました。MicrosoftのExcel上で動かすことができるので、特別なソフトウェアやハードウェアは必要としません。
今回のExcelファイルはローパスフィルターを例にした、FIRフィルターとIIRフィルターの動きを理解するためのデモファイル(Excelファイル)となります(ダウンロードには、Solution-Edge会員への登録(無償)およびログインが必要です)。
提供:ルネサス エレクトロニクス株式会社 / アナログ・デバイセズ株式会社
アイティメディア営業企画/制作:EDN Japan 編集部/掲載内容有効期限:2014年5月31日
Copyright © ITmedia, Inc. All Rights Reserved.