半導体の温故知新(3)――ムーアの法則は今後も続くが、その要求は弱まる:津田建二の技術解説コラム【歴史編】
「半導体集積回路に搭載されるトランジスタの数は毎年2倍で増えていく」。これが1965年に当時米フェアチャイルド・セミコンダクターにいたゴードン・ムーア博士が提案した、社会現象の「法則」です。のちにムーアの法則と呼ばれるようになった原型です。これが変質していく様子を見てみましょう。今の半導体技術の曲がり角に来ていることとムーアの法則は深く関係しているからです。
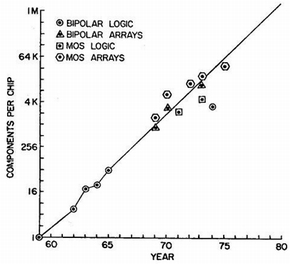
ムーア博士は、発表した10年後の1975年のIEDM(International Electron Device Meeting)において、集積回路のトランジスタ数が年率2倍で増えていたことを実証して見せました(図1)。この時から、この社会現象を「ムーアの法則」と呼ばれるようになりました。その後はペースが少し緩み、最近では2年に2倍のペースで集積度は増えていく、と変わりました。それでもムーアの法則には変わりません。
ただ、ムーアの法則には、大原則があります。それは研究所レベルでの集積度ではなく、商用化した製品のレベルでの集積度だということです。
デジタル時代に即した法則
なぜ、ムーアの法則が1965年以来ほぼ50年も続いてきたのでしょうか。それはトランジスタを1つのシリコンチップにたくさん集積するメリットが大きかったからです。トランジスタ1個のシリコンを製造するコストと100個集積したシリコンのコストがさほど違わなければ、100個集積した方が良い訳です。もちろん、集積することによって配線が短くなるため高速になる、と同時に消費電力も下がります。メリットは極めて大きくなります。
加えて、デジタル時代は2進法で表現するため、1ビットのスイッチの役割を果たすMOSトランジスタはできるだけたくさんある方が表現力は豊かになります。MOSトランジスタはバイポーラトランジスタと違って、トランジスタの当たりの面積が小さく集積化しやすいので、集積度の向上とデジタル化によって、MOSトランジスタは集積回路の主役になりました。
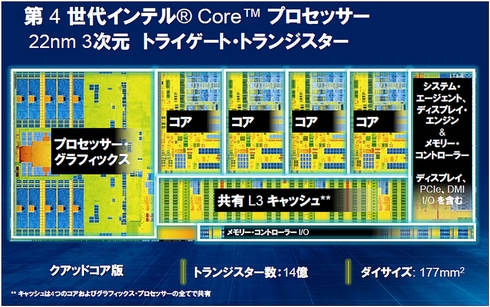
今、最も集積度の高いチップは、43億個のMOSトランジスタを集積したインテルの「Ivytown」でしょう。FPGAはロジックブロックの数で表現するため、トランジスタ数は明らかではありません。しかしSRAMをベースとしているため、最高集積度のFPGAも、億単位のトランジスタ数であることは間違いないでしょう。
ムーアの法則が微細化の進展と同意義に
ムーアの法則は、集積されるトランジスタ数について述べたものですが、トランジスタを集積するために必要な微細化技術の進展と集積度の向上は同じ歩調で進むようになりました。最初のマイクロプロセッサである4004のチップには集積されたMOSトランジスタは2300個、このチップは最小線幅10µmで製造されました。この最小線幅を7µm、5µm、3µm、2µm、1.5µm、1.25µm、1µm、0.8µm、0.5µm、0.35µm、0.25µm、0.18µm、0.13µm、90nmへと微細化してきて、現在は22nmの微細なマイクロプロセッサHaswellが量産されています。
集積度を上げるため、トランジスタ1個当たりの面積を小さくするとともに配線幅も細くしてきました。このため、ムーアの法則は、微細化の限界論や微細化技術と同じように語られるようになりました。ムーアの法則は間もなく止まるとか、微細化は限界に来る、といった言葉がそれを反映しています。
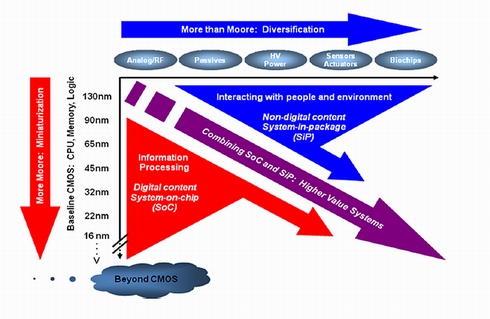
微細化の速度が緩和されてきたことで、ムーアの法則には2通りの道ができるといわれるように再定義されました。モアムーア(More Moore)とモアザンムーア(More than Moore)です。微細化のロードマップを描いてきたITRS(International Technology Roadmap for Semiconductors)委員会が2007年12月のセミコンジャパンの時期に併せて会合を開き、ムーアの法則を再定義しました(図3)。モアムーアは、新材料や3次元構造を採用して、ムーアの法則をさらに進展させる技術を表し、モアザンムーアはMEMSやアナログ回路、RF回路など、従来のデジタル回路以外の回路も集積して機能を追加する技術を表します。
しかし、微細化をさらに進めるという方向はかなり厳しくなってきています。というのは微細加工の決め手となるリソグラフィ技術のメドが立たなくなってきたからです。数年前まで20nm以下ではEUV(波長13.5nmのX線)リソグラフィ技術(図4)だといわれていましたが、その実用化が遅れています。最近では10nm未満になると見られています。従来のArFレーザーリソグラフィ技術でもトランジスタのパターンを加工するのに1つの露光で2回の工程を使うダブルパターニング技術が使われるようになっています。この方法では工程が2倍かかります。このため1時間あたりに処理できるウェーハの数、すなわちスループットが減少します。1回のリソグラフィであれば200枚/時のスループットがその半分に落ちるわけです。このためEUVリソグラフィのスループットがそれ以上求められます。EUVスループットを決めるのは、X線出力の増大です。現在はまだ40W強程度しかありませんが、100W以上を求められています。EUVの実用化がのびのびになっているのは、高出力のX線光源が完成していないからです。
ゴードン・ムーア博士が最初に定義したムーアの法則は、シリコン上に集積するトランジスタの数の傾向を表したものですが、シリコンではなく、ICパッケージ上に集積されるトランジスタ数と新しい定義をするなら、ムーアの法則は続くことになるでしょう。シリコンチップを3次元状に重ねていくという技術が実用化されている現在、ICを使うユーザーから見ると、ICパッケージに入っているシリコンチップが1個であろうと複数個であろうと関係ありません。ユーザーの欲しい機能が入っていれば良いからだです。
ムーアの法則は今後も続くか
今後、ムーアの法則は続くのでしょうか。これまでは、あらゆる用途において集積度が向上すればするほどメリットの大きかったのですが、もっと集積度を上げようという用途次第でしょう。例えば、テレビや音楽プレーヤーなどの単機能品では10億トランジスタを必要としないでしょう。あるいは洗濯機や冷蔵庫、電気釜のような用途でもそれほど大きな集積度は必要ありません。
しかし、スマートフォンのように機能を追加している製品では、集積度をもっと上げようとすると同時に、さらなる性能向上も求めています。この用途では集積度の向上はますます求められます。2013年、スマホ用のアプリケーションプロセッサを設計しているクアルコム社の技術マネージャーの方になぜ微細化するのか、聞いてみました。まだ十分な性能が得られていないからだ、と答えました。現在のスマホでブラウザを動かす時にサクサク動かないことがあります。この不満を解消するためにもっと微細にしてトランジスタ数を上げ性能を上げなければなりません、と言われました。つまりスマホの世界ではムーアの法則がまだ必要なのです。
以上の考察から、半導体製品の応用が広がるにつれ、集積度を上げる応用ばかりではなくなってきたことは確かです。しかし、集積度の向上がさらに求められる分野も確実にあります。全体的に、従来ほど集積度向上の要求は強くなくなっているため、集積化の進展は緩む方向にあるといえるでしょう。
Profile
津田建二(つだ けんじ)
現在、フリー技術ジャーナリスト、セミコンポータル編集長。
30数年間、半導体産業をフォローしてきた経験を生かし、ブログや独自記事において半導体産業にさまざまな提言をしている。
提供:ルネサス エレクトロニクス株式会社 / アナログ・デバイセズ株式会社
アイティメディア営業企画/制作:EDN Japan 編集部/掲載内容有効期限:2014年5月31日
Copyright © ITmedia, Inc. All Rights Reserved.