前回はデジタルICとロジックICの全体像を説明しました。今回はロジックICの基本である「論理回路」について解説します。
四則演算(算術演算)と論理演算
ここでは原点に立ち返って解説を始めます。まず「論理回路」とは何でしょうか。
「論理回路」とは、「論理演算」を実行する回路です。それでは「論理演算」とは何でしょうか。
小学校で習った「算数」を思い出してください。算数も「演算」です。算数をもう少し難しい用語で表現すると「四則演算」または「算術演算」となります。和算(足し算)、減算(引き算)、乗算(掛け算)、除算(割り算)の4種類(四則)による演算という意味です。演算の対象となるのは整数や実数、複素数などですね。
算術演算に対して「論理演算」とは、「真」と「偽」の2つの値だけを使う演算です。1個以上の「真」あるいは「偽」の入力から、1個の「真」あるいは「偽」を出力します。「真」、「偽」はいずれも単なる記号です。「高」、「低」の組み合わせや「1」、「0」の組み合わせで表現されることも少なくありません。実際、デジタルICやロジックICなどの半導体回路ではほとんどの場合、「1」と「0」の組み合わせを使っています。
論理演算の概念は、英国の数学者ジョージ・ブール(George Boole)が19世紀半ばに構築しました。このことから、論理演算は「ブール演算(Boolean Operation)」とも呼ばれています。
論理演算の実際
論理回路の基本となる論理演算は、「否定(NOT(ノット))」、「論理積(AND(アンド))」、「論理和(OR(オア))」の3つの演算です。
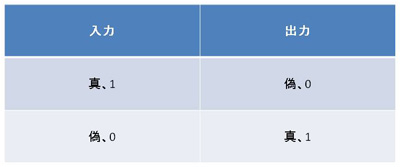
否定(NOT)は論理値を反転させる演算です。入力は1個だけで、「真」が入力のときは「偽」を出力し、「偽」が入力のときは「真」を出力します。
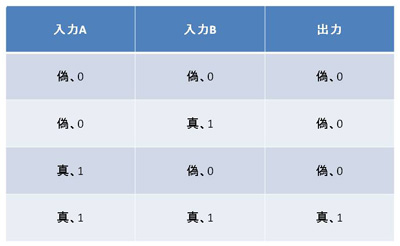
論理積(AND)は、入力が2個以上あり、全ての入力が「真」のときにだけ、「真」を出力します。そのほかの場合は「偽」を出力します。入力をAとBの2個にすると、論理積はA・BあるいはA×Bと表記されます。
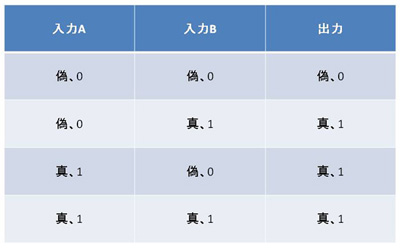
論理和(OR)は、入力が2個以上あり、いずれかの入力が「真」のときに、「真」を出力します。そのほかの場合、すなわち、全ての入力が「偽」のときにだけ、「偽」を出力します。入力をAとBの2個にすると、論理和はA+Bと表記されます。
論理回路は原理的には上記の3つの論理演算で全て表記できるのですが、シリコンのロジックICでは以下に付け加える2つの論理演算が重要です。
1つは「否定論理積(NAND(ナンド))」と呼ばれる演算です。論理積の出力を否定する演算で、入力の全てが「真」のときに「偽」を出力し、それ以外の場合には「真」を出力します。もう1つは「否定論理和(NOR(ノア))」と呼ばれる演算です。論理和の出力を否定する演算で、全ての入力が「偽」の場合にだけ、「真」を出力し、それ以外の場合には「偽」を出力します。
否定(NOT)回路とその動作
それでは、論理回路を電気回路で置き換えてみましょう。ここからは直観的に理解しやすいように、「真」は「1」、「偽」は「0」で表記します。また電気回路はCMOS回路に限定します。論理値の違いは「電圧の違い」で表現されます。「電源電圧」が「真」または「1」、「高」、「接地電圧」が「偽」または「0」、「低」を意味します。このことは非常に大切です。なぜかというと、これらが同じ意味であることを明らかにしないまま、論理回路やデジタル回路、トランジスタ回路を説明している記述を少なからず見かけるからです。
それでは、否定(NOT)、否定論理積(NAND)、否定論理和(NOR)の論理演算を実行する電気回路がそれぞれ、どのように記述されるかを順番に説明しましょう。なお、否定論理積(NAND)と否定論理和(NOR)の入力は2個とします。
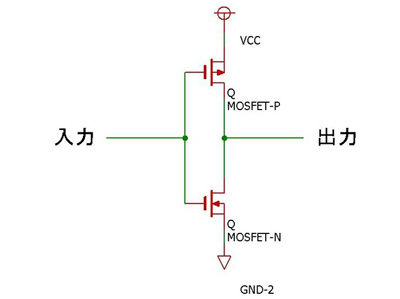
否定(NOT)回路は、1個のnチャンネルMOSトランジスタと1個のpMOSトランジスタで実現します。電源とpMOSトランジスタのソースを接続し、接地とnMOSトランジスタのソースを接続します。pMOSゲートとnMOSゲートを接続し、入力端子とします。pMOSトランジスタのドレインとnMOSトランジスタのドレインを接続し、出力端子とします。これでCMOSのNORゲートが完成しました。
CMOS NORゲートは以下のように動作します。入力が「1」、すなわち電源電圧のときはnMOSトランジスタがオン状態になり(同時にpMOSトランジスタはオフ状態となり)、出力は接地電位、つまり「0」となります。入力が「0」、すなわち接地電圧のときはpMOSトランジスタがオン状態になり(同時にnMOSトランジスタはオフ状態となり)、出力は電源電位、つまり「1」となります。
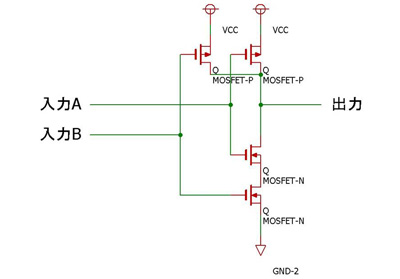
否定論理積(NAND)回路とその動作
否定論理積(NAND)回路は、否定(NOT)回路にnMOSトランジスタとpMOSトランジスタを1個ずつ加えることで実現します。2個のpMOSトランジスタは並列に、2個のnMOSトランジスタは直列に接続します。nMOSゲートとpMOSゲートが1本ずつ対になるように接続され、2本の入力を形成します。2個のpMOSトランジスタのドレインと1個のnMOSトランジスタのドレインが接続されて出力端子となります。これでNANDゲートが完成しました。
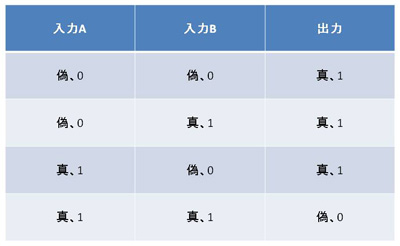
NANDゲートでは2本の入力の両方が「1」、すなわち電源電圧になると2個のnMOSトランジスタの両方がオン状態となり(同時に2個のpMOSトランジスタの両方がオフ状態となり)、出力は接地電圧、つまり「0」となります。入力のどちらかが「0」、すなわち接地電圧になると「0」入力のpMOSトランジスタがオン状態になるとともに、「0」入力のnMOSトランジスタがオフ状態となり、出力は電源電圧、つまり「1」となります。
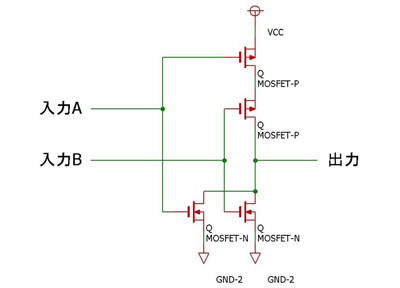
否定論理和(NOR)回路とその動作
再び否定(NOT)回路に戻りましょう。否定論理和(NOR)回路も、否定(NOT)回路にnMOSトランジスタとpMOSトランジスタを1個ずつ加えることで実現します。ただしNAND回路とは違い、2個のpMOSトランジスタは直列に、2個のnMOSトランジスタは並列に接続します。nMOSゲートとpMOSゲートが1本ずつ対になるように接続され、2本の入力を形成します。1個のpMOSトランジスタのドレインと2個のnMOSトランジスタのドレインが接続されて出力端子となります。これでNORゲートが完成しました。
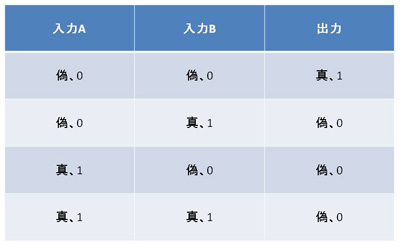
NORゲートでは2本の入力の両方が「0」、すなわち接地電圧になると2個のpMOSトランジスタの両方がオン状態となり(同時に2個のnMOSトランジスタの両方がオフ状態となり)、出力は電源電圧、つまり「1」となります。入力のどちらかが「1」、すなわち電源電圧になると「1」入力のpMOSトランジスタがオフ状態になるとともに、「1」入力のnMOSトランジスタがオフ状態となり、出力は接地電圧、つまり「0」となります。
シリコンICではトランジスタ数の少ない回路を使う
ANDゲートやORゲートなどは、NANDゲートやNORゲートなどに比べると直観的に理解しやすい回路です。しかしシリコンICの世界では、NANDゲートとNORゲートを基本回路として大規模な論理回路を構築するのが普通です。なぜかというと、論理ゲートの実現に必要なトランジスタの数が違うからです。
例えばANDゲートは、通常はNANDゲートの出力にNOTゲートを接続して実現します。すぐ分かるのですが、NANDゲートの実現には4個のMOSトランジスタを必要とするのに対し、ANDゲートの実現には6個のMOSトランジスタを必要とします。トランジスタ数ですと1.5倍になります。この違いはシリコン面積の違いに大きく影響します。半導体製造ではシリコン面積をなるべく狭く小さくする、すなわち、なるべく少ない数のトランジスタで電気回路を実現することが最優先されます。このため、シリコンICの論理回路ではANDゲートやORゲートは使われず、NANDゲートとNORゲートを使っています。
組み合わせ論理回路と順序論理回路
れまで説明してきたNOTゲートやNANDゲートなどの論理ゲートは、入力の論理値によって出力の論理値が決まります。このような回路を「組み合わせ論理回路(Combinational Logic)」または「組み合わせ回路」と呼びます。
これに対して、回路の内部状態(内部の論理値)と入力の論理値によって出力が決まる論理回路も存在します。このような論理回路を「順序論理回路(Sequential Logic)」または「順序回路」と呼びます。
次回はこの「順序回路」について解説します。
提供:日本テキサス・インスツルメンツ株式会社
アイティメディア営業企画/制作:EDN Japan 編集部/掲載内容有効期限:2013年3月31日
Copyright © ITmedia, Inc. All Rights Reserved.