デジタル・フィルターとアナログ・フィルター(3)――デジタルフィルターの使い方:ソリューションライブラリ
データコンバータ(A-DコンバータやD-Aコンバータなど)は、アナログ信号処理とデジタル信号処理の間を橋渡しする素子です。デジタル・フィルターについて解説してきているこの入門編で、少し実際のフィルターの使い方についてお話ししたいと思います。
ノイズを取り除くフィルター
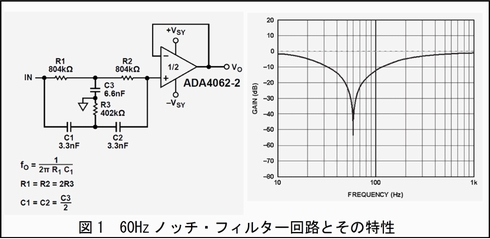
フィルタリングというとすぐイメージとして浮かぶのは、ノイズに埋もれた信号を取り出すために、必要以外の周波数帯域成分(これがノイズです)をそぎ落とすために使用するフィルターです。例えば、図1に示すノッチ・フィルターの一例です。
これは微小信号(例えば心電図や熱電対信号、センサー出力など)を増幅して信号処理を行おうとしたとき、アナログ入力の配線に結合してのってくる50/60Hzのライン・ノイズを取り除くために、この周波数を抑圧するバンド・エリミネーション・フィルター(BEF)の一種です。BEFは、バンド・リジェクト・フィルターと呼ぶ場合もあり、日本語では帯域阻止フィルターとなります。
このフィルターは、ツインTノッチ・フィルターと呼ばれ、図1の定数で60Hz(ノッチ周波数と呼びます)のノイズを除去します。図1に示された計算で定数を変更すれば50Hzノッチ周波数のフィルターも可能です。フィルターに使われているRやCの値はマッチングが重要で、これらがずれるとノッチ周波数のずれになります。このフィルターは完全にアナログ素子だけで構成されていますが、同じことはデジタル・フィルターでも実現可能です。
ただし、考慮しなければならないことがあります。それは前回に述べた、ダイナミック・レンジと信号/ノイズの比率です。50/60Hzのノイズが大きいと(信号より大きい場合が一般的)、A-D変換の際にノイズ成分にダイナミック・レンジを取られ信号そのもののレンジが広く確保できなくなるということです。
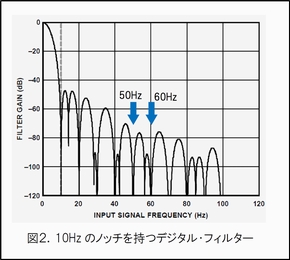
その場合はまずアナログ・フィルターでこのライン・ノイズを除去します。しかしシグマ・デルタA-Dコンバータのように分解能が高くダイナミック・レンジが広い場合は、A-D変換後のデータでフィルター処理することも有意性があります。この典型的な例が、シグマ・デルタA-Dコンバータのデジタル・フィルターによるライン・ノイズの除去です。移動平均フィルターの設定によりノッチ周波数を50/60Hzにプログラムし、ノイズの影響を除去するものです(図2参照)。このノッチ周波数を、両社の周期の公倍数としてうまく選ぶと、50Hzと60Hzを同時に除去するフィルターが構成できます。例えばノッチを10Hz(100m秒)に選ぶと、50Hz/60Hzを同時にフィルタリングできます。
上に述べた使い方は、ノイズ(必要な信号以外の全ての周波数成分)を取り除くためのフィルターということですが、以下ではこれとは少し異なる、特にデジタル・フィルターの重要な応用について解説します。
その他のデジタル・フィルターの応用
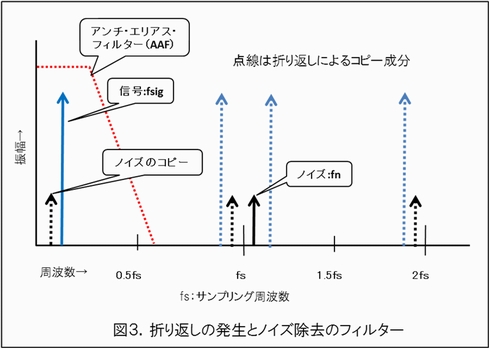
前回のアンチ・エリアス・フィルター(AAF)の解説部分を思い出してください。多少繰り返しになりますが、図3にAAFの必要性について簡単に示しました。A-D変換する前にサンプリングにより折り返される高い周波数に存在するノイズを、あらかじめ取り除く目的でアナログ・フィルターがAAFとして用いられます。
図3は理論的な図ですが、実際は折り返しが生じるには、ある条件が必要です。それはこのA-Dコンバータ(あるいはサンプラー)のアナログ入力帯域が、高い帯域にあるノイズの周波数まであることです。入力帯域がノイズの周波数であるfnより低ければ、このノイズは入力信号として認識はされず、サンプラーはこのノイズをサンプリングすることはできません。最近のA-Dコンバータのデータシートには、ほとんどの場合このアナログ入力帯域の性能がスペックとして記載されているはずです。一例として「AD9200」のデータシートの一部を図4に示します。AD9200は、A-D変換のレートが最高20MHzなのに、アナログ入力帯域は、それを上回る300MHzもあります。このA-Dコンバータの場合、変換周波数より高い帯域にある信号が、サンプリングにより低い周波数に折り返してくることになります。
A-D変換の教科書的には、サンプリング周波数(変換周波数)“X”Hzのデータ変換システムでは、もとの信号に含まれるX/2Hzまでの周波数成分を再生することはできるとなっています(ナイキストのサンプリング定理)。これより広い入力帯域は、その帯域のノイズを拾ってしまってそこに折り返しが生じるという不都合があるようにみえますが、実はこの現象を使った周波数変換の応用が、最近では非常に多く使われるようになってきました。ここではデジタル・フィルターが大活躍しています。アナログ・フィルターではこのマネは無理があり、非実用的です。
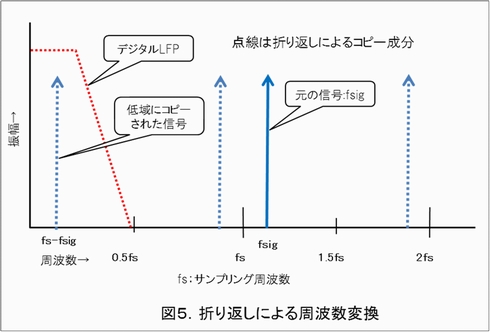
図5を見てください。
この図のシステムでは、A-Dコンバータのサンプリング周波数fsより高い帯域に必要とする信号fsigがあります。もしA-Dコンバータのアナログ入力帯域が、この信号fsigより広ければ、この信号はfsでサンプリングされた際にfs/2の帯域に区切られた周波数区分(ナイキスト・ゾーンと呼んでいます)毎に、鏡で映したように折り返されコピー成分が生じます。このコピーは、オリジナルの信号と全く同じ振幅を持っています。ということは、低い周波数に折り返されたコピーを、デジタル・フィルタリングにより取り出せば、元の信号を周波数変換したことになります。
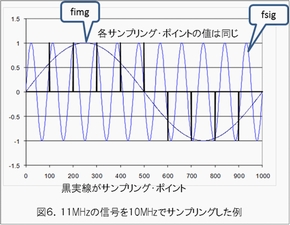
これを時間軸で表したものが図6です。高い周波数にある信号fsigと、そのイメージであるfimgは、同じ周期でサンプリングするとそのデータの値が全く同じになることが示されています。常にfsigとfimgの交点が、サンプリングのポイントになっています。このポイントをA-D変換するのですから、デジタル・データは同じ値になります。
今は単一スペクトラムの信号で考えていますが、これが変調され、ある程度の帯域を持った信号でも同じことができます。高い周波数の信号をミキサーやIFフィルターなどでアナログ処理をしていることが、デジタル処理をできることになります。ここでこの折り返し信号を取り出すためには、デジタル・フィルターが必要になります。図5のベースバンドに落ちてきた信号は、A-D変換されたデジタルコードによるデータとなっているので、これを処理するにはデジタル・フィルターによる計算が必要になるからです。ここではデジタル・ローパス・フィルターですが、システムの仕様によって、DC成分が不要であればバンドパスを使用します。
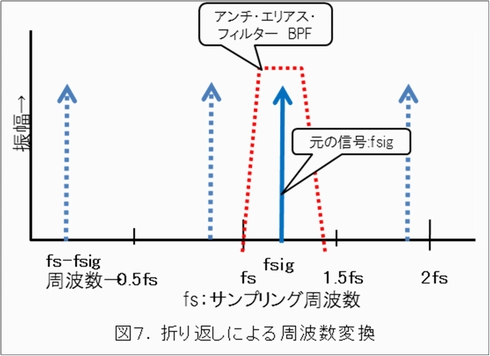
このようにサンプリング周波数より高い帯域にある信号を、折り返しを利用して周波数変換し、低域での信号処理をするやり方を、アンダーサンプリング(Under Sampling)と呼びます。シグマ・デルタA-Dコンバータなどで使われるオーバーサンプリング(Over Sampling)の逆になります。この信号処理でも、帯域外のノイズを取り除き、ダイナミック・レンジを最適化するためには、サンプリングの前にアナログのアンチエリアス・フィルターが必要です。もう想像がつくと思いますが、図7のように信号帯域外のノイズ除去のため、バンドパス構成のAAFを使います。
アンダーサンプリングを用いたデータ変換システムは、通信機器をはじめとするシステムに多用されています。これらのシステムは、信号の存在する帯域は高いところにあるのですが、その帯域幅が限られていると、A-D変換することで周波数変換することができるので、アナログ・ミキサーなどのIF段を減らすことができ、温度ドリフトなど要因を減らすことができます。
周波数変換する場合の注意
さてA-D変換とデジタル信号処理で周波数変換が可能と述べていますが、実際にこのやり方を応用しようとする際には、A-Dコンバータの特性やアナログのフロントエンドに注意を払う必要があります。
A-Dコンバータのアナログ入力帯域については、先に述べたようにもともとの信号が存在する高い周波数まで延びていなくてはなりません。では帯域だけが重要かというと、そうでもありません。その帯域でのA-D変換の結果が、十分な意味を持つ精度でなければなりません。具体的には、変換結果のSN比、すなわち有効ビット(ENOB:Effective Number Of Bit)や歪み率(Harmonic Distortion)などのコンバータのAC変換精度に関する特性が、自分が必要としている性能に合っているかという判断が重要です。A-D変換結果のデータにー40dBの歪みが含まれていれば、コピーされた折り返し成分にもこの歪みが含まれています。コンバータ内部ではなく、外部から入ってくる広帯域のノイズについては、フィルタリングにより改善することができます。
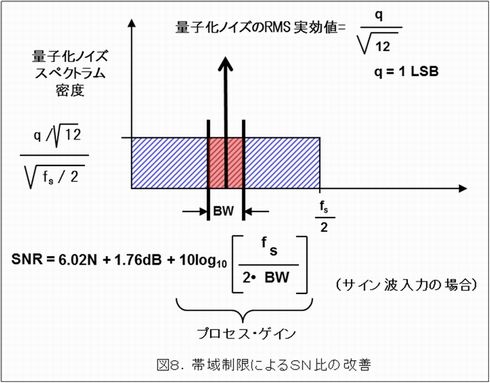
例えばアナログ入力帯域が100MHzのA-Dコンバータは、逆に見れば100MHzまでの広帯域ノイズを拾ってA-D変換して出力データに加えるということになります。フィルターより信号周辺に帯域を絞るとそれ以外のノイズも抑圧することになるので、全体としてのSN比の改善に寄与します。またA-D変換時に発生する量子化ノイズも、この帯域制限により改善します。この寄与分をプロセス・ゲインと呼んでいます(図8参照)。
多ビットデータに変換
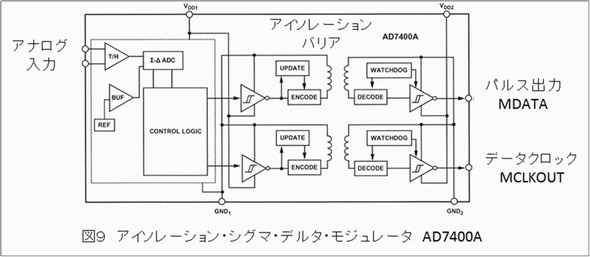
もう1つデジタル・フィルターの活躍する場面の例としてあげられるのは、シグマ・デルタ・モジュレータの出力である密度変調されたパルス列をフィルタリングして、多ビットのデータに変換する回路です。最近では、この機能が内蔵されたシグマ・デルタA-Dコンバータが全盛ですので、このモジュレータ部分だけという素子は少なくなっているのですが、図9にそのモジュレータ素子の例を示します。このモジュレータは、内部に磁気結合による絶縁バリアを持っています。
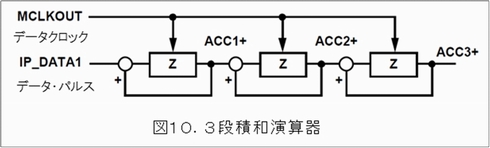
このパルス列をデジタル・フィルター(積分器)とデシメータ(微分器を含む)を通して多ビット(例えば16ビット)データに変換します。デジタル・フィルターはSINC関数を使ったものが多く、図のAD7400ではSINC3フィルターが推奨されています。SINC3は、SINC動作を3段接続して作ります。積分器部分は、単純な3段アキュムレータで、その幅は処理するデータ長に合わせます。ここでは、出力レジスタとWORD_CLK以外は24ビット長です(図10参照)。
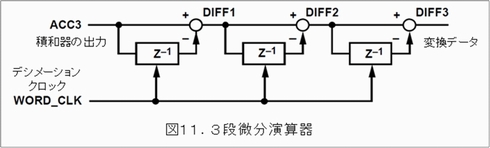
ここでは、モジュレータのクロック速度(MCLKOUT)で積和演算を行っています。Zは1つ前の演算結果です。ただし積和の計算が飽和しないように、パルスがLの時は−1として補数により引き算をします。これはMCLKOUTクロックによるIIRの演算となり、出力Acc3は、同じクロックレートで出てきます。これらのアキュムレータ・レジスタは、RESETが入るとみな0にリセットされます。このAcc3の出力をデシメーション(間引き)して、出力データレートを下げ、変換データとして出力します。この部分は、3段の微分回路(FIR)を利用して、図11のように構成されています。
ここではデータレートを下げるために、MCLKOUTより遅いWORD_CLKを使用します。デシメーションの比率は、このWORD_CLKにより決まります。このクロックのカウンターが8ビット長であれば、最大MCLKOUTの1/256の周波数までデータレートを遅くすることができます。RESETが入ると、DIFF1などの各レジスタは0に設定されることは同じです。ここでは1つ前のデータと今のデータの差分値(微分)をWORD_CLKに従って計算します。これを3段カスケードして、最終結果DIFF3を変換データとします。各段を3回繰り返しているので、この結果はSINC3フィルターを通したものとなります。
ここでは最初の入力が1ビットのパルス列でしたが、マルチビットのデータでも同じことができます。シグマ・デルタADコンバータは、かつて1ビット・コンバータと呼ばれていましたが、最新のものは内部モジュレータに1ビット・コンバータを使う例はほとんどなく、3〜5ビット程度のエンコーダ(高速のA-Dコンバータ、多くはフラッシュA-Dコンバータ)を使用しています。これは、強力なデジタル・フィルターでなくても1ビットに比べて高精度、広ダイナミック・レンジを容易に実現できるからです。
エンジニアの技量が試されるフィルタリング
フィルタリングは、信号処理の最も重要な要素の1つです。それだけにさまざまな実現方法があり、どの構成を使うかということは、設計エンジニアの技量が大きく試されるところです。ここではいくつかの例をあげてきましたが、デジタル・フィルターをうまく使うと高性能な信号処理システムを、構成することができます。しかし元がアナログ信号である場合、そのデータ変換をどのポイントで行うのか、またアナログ信号処理と組み合わせて性能を最適化するには、どのように双方の特性を生かす構成とするか、設計者のセンスが大きく影響します。その入門編として、ダウンロードコンテンツにあるプログラムを利用して、デジタル・フィルタリングとそれをサポートするアナログ・フィルタリングについて実際に動作を確認いただければ理解も早いと思います。
提供:ルネサス エレクトロニクス株式会社 / アナログ・デバイセズ株式会社
アイティメディア営業企画/制作:EDN Japan 編集部/掲載内容有効期限:2015年5月31日
Copyright © ITmedia, Inc. All Rights Reserved.