前回(第3回)は電磁気(電流と磁界)と力(運動)の関係をテーマに、モーター(電動機)とジェネレーター(発電機)の基本原理を説明しました。今回(第4回)は電磁気から離れ、電気回路に戻ります。抵抗やコイル(インダクタンス)、コンデンサなどが存在する電気回路で、電圧信号と電流信号がどのように変化するのか。その様子を分かりやすく解説します。
まず、第1回でご説明した「オームの法則」と「キルヒホッフの法則」は、覚えておられますでしょうか。忘れている方は先に進む前に、第1回のテキストを読み返してください。
電気回路の基本素子と言えば、抵抗とインダクタンス、コンデンサですね。これらは「受動部品(じゅどうぶひん)」あるいは「受動素子(じゅどうそし)」と呼ばれています。英語ではPassive Components(パッシブ・コンポーネンツ)と表記しています。半導体商社や電子部品商社、電子部品メーカーなどの担当者によっては、省略して「パッシブ」と呼ぶこともあります。
受動部品と対比する用語には、「能動部品(のうどうぶひん)」あるい「能動素子(のうどうそし)があります。英語ではActive Components(アクティブ・コンポーネンツ)と表記しています。単に「アクティブ」と呼ぶこともあります。代表的な能動部品はトランジスタとダイオードです。
抵抗とインダクタンスの表記と呼び方
それでは、抵抗とインダクタンスが存在する回路について考えてみましょう。
抵抗はレジスタンス、またはレジスタと呼ぶこともあります。ただしレジスタは論理回路の「レジスタ」と紛らわしいのでお薦めしません。「抵抗」あるいは「抵抗器」、「抵抗素子」と表記しましょう。
インダクタンスはインダクタ、またはコイルを呼ぶこともあります。コイルと表記すると銅ワイヤを円筒状にぐるぐる巻きにしたものを想像しがちですが、電気回路では寄生的な成分(本来の目的以外の電気的な回路成分:寄生抵抗や寄生インダクタなど)も扱うので、厳密にはインダクタンスまたはインダクタと記述すべきでしょう。
記号で表記するときは、「抵抗」はR(アール)、「インダクタンス」はL(エル)と略記します。電気回路に関する会話ではそれぞれ、「アール」および「エル」と略して呼ぶことが珍しくありません。
乾電池にRとLを直列接続したときの電流
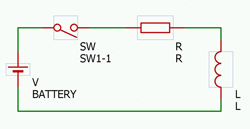
それではRとLが混在する簡単な電気回路で、電圧信号と電流信号のふるまいを考えてみましょう。乾電池や二次電池などの直流電圧源Vと、スイッチSW、抵抗R、インダクタンスLが直列に接続された閉回路を想定します(図1)。始めはスイッチSWが開放(オフ)状態です。
ここでスイッチSWを短絡(オン)状態にします。直流電圧源Vの電圧Vが抵抗RとインダクタンスLに加わります。抵抗Rの両端に加わる電圧をvR、インダクタンスLの両端に加わる電圧をvLと定義しますと、VはvRとvLの合計値で、常に一定です。
V=vR+vL
インダクタンスLの両端に加わる電圧vLは、閉回路を流れる電流iの時間微分にLを掛けた値となります。抵抗Rの両端に加わる電圧vRは、電流iにRを掛けた値です。スイッチSWをオンにした直後では電流iはゼロから流れ始めるので、電流iの時間微分が高く、電流iそのものは低い値に留まっています。したがって普通は、vL>vRです。
時間がほんの少し経過すると電流iが増えます。vRが増加し、vLが減少します。電流iの時間微分も下がります。電流iは増加しながら、その時間微分を減少させていきます。そして時間が無限大に達すると、電流iの時間微分(電流iの時間当たりの変化)はゼロになり、電流iはVをRで割った値となります
電流i(時間は無限大)=V/R
この式はオームの法則そのものであることが分かります。ここで「時間が無限大」になった状態を「定常状態」、時間がゼロから無限大になるまでの状態を「過渡状態」と呼びます。定常状態では、インダクタンスLは電気回路に何の影響も与えていないことが分かります。
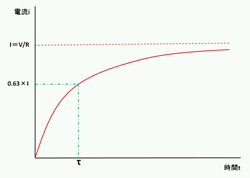
定常状態での電流iをIと表記しましょう。LとRの大小関係が、電流iがIに近付く早さ(定常状態に近付く早さ)を決めます。LとR、V、iに関する微分方程式を解くと、電流iは「L/R」を係数とする指数関数の逆数で、時間tとともに増加していくことが分かります。この「L/R」を時定数τ(タウ)と呼びます。時間がτのときに、電流iはおおよそIの0.63倍の値となります。Lが小さく、Rが大きいと、電流iは素早く立ち上がり、定常状態に近付きます。
提供:日本テキサス・インスツルメンツ株式会社
アイティメディア営業企画/制作:EDN Japan 編集部/掲載内容有効期限:2013年3月31日
Copyright © ITmedia, Inc. All Rights Reserved.