第6回では、抵抗やインダクタンス(コイル)、コンデンサ(キャパシタ)などが存在する電気回路で、電流信号が時間とともに、どのように変化するのか。その様子を分かりやすく解説します。
前々回(第4回)は、抵抗とインダクタンス(コイル)を直列接続した回路、前回(第5回)は抵抗とコンデンサ(キャパシタ)を直列接続した回路で過渡現象をご説明しました。
インダクタンスの働きとコンデンサの働き
前回と前々回から、インダクタンスとコンデンサでは働きが大きく違うことを学びました。抵抗とインダクタンスを直列接続した回路では、電源を投入するとインダクタンスが電流を妨げるので、電源投入時(時間t=0)の電流iはゼロになっています。時間の経過とともに電流iは増加し、時間が無限大(t=∞)になると電流iは一定値Iとなります。この電流I(t=∞)は電源電圧Vを抵抗Rで割った値V/Rに等しく、回路には見掛け上、インダクタンスは存在しません。
一方、抵抗とコンデンサを直列接続した回路では、電源を投入すると電流が勢いよく流れ出します。電源投入時(t=0)の電流iは電源電圧Vを抵抗Rで割った値V/Rに等しく、回路には見掛け上、コンデンサは存在しません。時間の経過とともに電流iは減少し、時間が無限大(t=∞)になると電流iはゼロになります。
これらの事柄から分かるのは、電源投入直後はインダクタンスLの影響が大きく、時間が経過するとコンデンサCの影響が大きくなるということです。
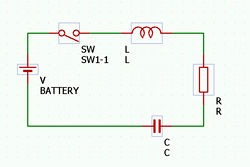
乾電池にLとRとCを直列接続したときの電流の変化
それではRとLとCを直列に接続した電気回路で、電流信号と電圧信号のふるまいを考えてみましょう。
乾電池や二次電池などの直流電圧源Vと、スイッチSW、インダクタンスL、抵抗R、コンデンサCが直列に接続された閉回路を想定します(図1)。始めはスイッチSWが開放(オフ)状態です。コンデンサCには電荷が蓄えられていないものとします。
ここでスイッチSWを短絡(オン)状態にします。直流電圧源Vの電圧VがインダクタンスLと抵抗R、コンデンサCに加わります。インダクタンスLの両端に加わる電圧をvL、抵抗Rの両端に加わる電圧をvR、コンデンサCの両端に加わる電圧をvCと定義しますと、VはvLとvR、vCの合計値で、常に一定です。
V=vL+vR+vC
スイッチSWをオン状態にした(t=0)のとき、第4回のLR直列回路ではvL=V、vR=0であることを、第5回のCR直列回路ではではvC=0、vR=Vであることをご説明しました。今回のLRC直列回路では、t=0のときには電流が流れていません。このため、vL=V、vR=0、vC=0です。次の瞬間(t>0(tは0に近い))になると、電流が流れ出してvLが減少し、vR>0、vC>0となります。この時点からは、LとR、Cの大小関係によって電流iの振る舞いが大きく違ってきます。
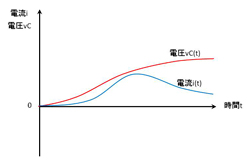
最初は、RがLよりも大きく、Cが比較的大きな場合を考えます。定量的には、「Rの2乗/(2L)の2乗>1/(L×C)」という関係が成立する場合です。この条件で微分方程式を解くと、電流iは時間tの経過とともに上昇し、一度は極大値に達したあと、ゆっくりとゼロに向かって下がっていきます。コンデンサCの両端に加わる電圧vCは滑らかに上昇し、一定値に近付きます。この状態を「過減衰(over damping)」と呼びます。
LとCが電流の振動を作り出す
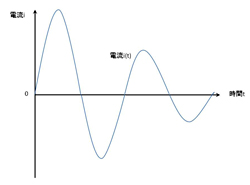
次に、RがLよりも小さく、Cが比較的小さな場合を考えます。定量的には、「Rの2乗/(2L)の2乗<1/(L×C)」という関係が成立する場合です。この条件で微分方程式を解くと、電流iは時間tとともに「急激に」上昇し、極大値に達したあと、「急激に」減少します。電流iの急激な上昇によってコンデンサC両端の電圧vCは直流電圧源の電圧Vを超えてしまいます。続いてコンデンサCは放電を初め、電流iは逆方向に流れ出します。i<0(逆方向電流)となります。逆方向電流は極小値に達した(vC=Vに達した)あと、再び上昇を始めます。そして極大値(前の極大値よりは低い値)に達したあと、再び減少します。
このように電流iは増加と減少を繰り返しつつ、ゼロへと近付いて行きます。コンデンサC両端の電圧vCは直流電圧源の電圧Vを中心に振動しつつ、時間の経過とともにVへと収束します。この状態を「減衰振動(damped oscillation)」と呼びます。
電流波形の減衰が最も早くなる条件
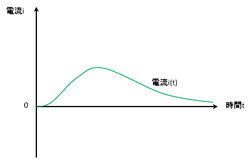
それでは、「Rの2乗/(2L)の2乗=1/(L×C)」である場合を考えましょう。この条件で微分方程式を解くと、電流iは時間tとともに上昇し、極大値に達したあと、ゆるやかに減少していきます。電流が上昇する割合(スルーレート)は「減衰振動」よりも低く、「過減衰」よりも高いです。電流iが極大値に達する時間は「過減衰」よりも短く、早く減衰していきます。言い換えると、電流iが最も早く減少する条件が「Rの2乗/(2L)の2乗=1/(L×C)」なのです。
このとき電流iは振動を起こさないぎりぎりの高い速度で増大し、素早く減衰していきます。この状態を「臨界減衰(critical damping)」と呼びます。
このようにLRC直列回路では、回路定数の大小関係によって過渡状態の電流iが異なる振る舞いをします。いずれにしても時間が無限大のときには電流iはゼロになるのですが、ゼロに至るまでの波形は大きく違っています。抵抗Rが支配的な場合は過減衰となり、インダクタンスLとコンデンサCが支配的な場合は減衰振動となります。そして特定の条件を満足すると、臨界減衰となります。
提供:日本テキサス・インスツルメンツ株式会社
アイティメディア営業企画/制作:EDN Japan 編集部/掲載内容有効期限:2013年3月31日
Copyright © ITmedia, Inc. All Rights Reserved.