デジタルフィルターとアナログフィルター(1)――デジタルフィルター超入門編:ソリューションライブラリ
これから数回にわたり、アナログ信号よりある帯域の成分を取り除き、必要な信号成分だけを取り出す目的で使用される、信号処理用のフィルターについて紹介していきます。今回は、フィルター処理の中で、アナログ信号の状態で使用するアナログ・フィルターと一度デジタル値に変換してから処理を行うデジタル・フィルターについて、その特長の違いや組み合わせなどを解説していきます。
フィルターという言葉を聞いてイメージすることは、人によりその仕事の性質上さまざまだと思います。ある人はRF用のフィルターを想像し、ある人はスイッチング電源用のライン・フィルターをイメージするかもしれません。ここでお話しするフィルターは、アナログ信号よりある帯域の成分を取り除き、必要な信号成分だけを取り出す目的で使用される、信号処理用のフィルターについてお話をしていきたいと思います。またフィルター処理の中で、アナログ信号の状態で使用するアナログ・フィルターと一度デジタル値に変換してから処理を行うデジタル・フィルターについて、その特長の違いや組み合わせなどついて話を進めていきたいと思います。
はじめに図1に示すアナログ信号処理の簡略化したモデルを見てください。
左のアナログ側と右のデジタル側の信号処理があり、その間にデータ・コンバータがあります。アナログのフィルターは当然左の側で使われますが、ここでは信号に対してリアルタイムの処理が行われます。信号の増幅や減衰、レベルシフト、インピーダンス変換、四則演算、信号変換(電流・電圧変換など)、積分/微分などさまざまなアナログ信号処理回路が考えられますが、アナログ・フィルターもこの信号処理の1つです。デジタル信号処理は、アナログ信号が一度デジタル値に変換された後に、数値計算として信号の処理を行い、必要であればDAコンバータでアナログ値に戻して出力します。デジタル信号処理でも、計算によりフィルター回路を構成することができます。しかも場合によっては、リアルタイムではなく一度メモリの中に取り込んだ信号データを使って後で信号処理をするということも可能です。
信号のフィルタリングはアナログ、デジタル双方で可能です。しかしそれぞれに異なった特徴があります。その比較は、表1をご覧ください。
アナログ・フィルターの伝達特性を決めるのは、使われる部品の性能、特性に100%依存します。例えばカットオフ周波数は、使う受動部品の公称値からの誤差によりずれ、また使用温度が変わればそれによって定数が変化し、特性がドリフトします。OPアンプなどを利用したアクティブ・フィルターでは、そのアンプの特性やドリフトによって特性に影響が出てきます。
デジタル・フィルターは、これとは逆に性能はフィルターのアルゴリズムや分解能、計算精度などにより決まりますが、一度設定されれば温度ドリフトなどでずれるということはありません。アナログ・フィルターの場合は、そのフィルターの応答や性能を変えようとするとハードウェア全体を変えなければなりませんが、デジタル・フィルターの場合ハードウェアの変更はほとんど不要で、プログラミングの変更で対応することになります。処理する信号に合わせてフィルターの特性をかえて柔軟な対応が可能です。このように見るとデジタル・フィルターのほうが優れているように見えますが、使う場所やアプリケーションによってそうでもないことが分かります。双方の特長をよく理解して使うことが重要です。
デジタル・フィルター処理は、あくまでもAD変換の結果のデータが正しいという前提がないとなり立ちません。コンバータのダイナック・レンジを超えるような信号が入れば、いかにデジタル処理でも正しい結果は出ません。従ってデジタル・フィルター処理の1つのキーポイントは、デジタル値に変換する際にいかにSN比の高い(ダイナミックレンジの広い)データを得られるかというということになります。1つの例を図2に示します。
ここではアナログ信号に、大きなDCのオフセット(ノイズ)がのった状態を示します。デジタル処理でこのDCオフセットを取り除く(フィルタリングする)ことはできますが、これだと信号として使えるコンバータのダイナミックレンジは半分で、変換後に出てくるデータのSN比は最初から―6dBということになります。この信号を使ったデジタル処理ではこの変換データ以上の精度はできないのですから、初めから−6dBのペナルティを負っていることになります。DC成分が不要であるなら入力にDCカットのフィルターを付けたり、DCのレベルシフト回路で取り除くなどのアナログ処理をすれば、それだけでAD変換部分のダイナミックレンジは2倍になり、SN比は6dB向上します。
もう1つの例は、より深刻なものです。図3は、ある信号faを周波数fsでサンプリングした時の一例です。
サンプリングを行うと、必ず折り返し(エリアシング:Aliasing)という現象が起きます。しばしば誤解されますが、AD変換を行うと折り返しが起こるように考えられていますが、実際はAD変換をしないでもサンプリングをした段階でこの現象が起きます。
1/2fsの周波数幅を持ったナイキスト・ゾーンに信号がコピーされ、繰り返し現れるようになります。たまたまfnという高い周波数にノイズが存在すると、このノイズもコピーされ、それぞれのナイキスト・ゾーンに折り返されます。この図では最初のナイキスト・ゾーンの信号のすぐそばに折り返されています。このノイズはAD変換されて出力されますが、これをデジタル・フィルターで取り除こうとしても、信号と周波数が近いため至難の業です。これを避けるには、サンプリングをする前にアナログ・フィルターで帯域制限し、2番目以上のゾーンにあるノイズを抑圧する必要があります。これをアンチ・エリアス・フィルターと呼びます。デジタル処理をする前にアナログ・フィルターで取り除かないと、やはりSN比が劣化し、デジタル・データの純度が低下します。
デジタル・フィルターでは、アナログ・フィルターができる機能はほとんど実現可能ですが、前の2例のように実用的にはアナログ・フィルターの力を借りないといけない場面が数多くあります。それぞれのTPOを考察することが重要で、その目的は、信号経路のダイナミックレンジを最大化し、信号の純度をいかに最適化するということになります。
デジタル・フィルターで最も簡単なものは、単純な移動平均を計算する回路(アルゴリズム)です。サンプリングされAD変換されたデータの、連続する幾つかを加算して平均化したものを1つのサンプル・データとするものです。例えば4個のデータを加算して平均化すると、そのデータはサンプル間隔の4倍の区間の平均値となります。その周波数応答(回路のゲイン特性)は、図4のようになり、ロ-パス・フィルターを形成しているのが分かります。
このローパス・フィルターは、サンプルの数とその間隔(サンプリング周波数)により特性が決まりますが、サイドローブ(最初のカットオフの外側の特性)が盛り上がり、一番大きなものでは信号の10%ぐらいのゲインになりますので、この辺りに不要なノイズがある場合は、あまり良いフィルターとはいえないかもしれません。振幅の落ち込む(除去される)底の周波数を、ノッチ周波数と呼びます。このノッチ周波数を50Hzや60Hzに合わせて設計すると、ラインからのノイズ(ハム)を抑圧することができます。また周波数応答を見るとSin(x)/xになっているので、これをsinc応答フィルターと呼んでいます。この移動平均を式で示すと、図5のように表されます。
n番目の出力データ=(an+an-1+an-2+an-3 …… +an-m)/(m+1)
an=n番目のサンプル・データ、an-1=n-1番目のサンプル・データ … an-m=n-m番目のサンプル・データ
m+1=平均化のサンプル数
移動平均フィルターは、過去の有限の値のサンプリング値を用いて計算し、1つ次の計算では、新しいサンプルを計算に反映する代わり、1つ前の計算データの最も古いものを除き、出力に反映させません。 このタイプのフィルターをFIR(Finite Impulse Response)フィルターと呼びます。有限のデータを使うのでFIRですが、これと対照的に過去のデータを全て使いながら計算するフィルターをIIR(Infinite Impulse Response)フィルターと呼びます。
ここで1つ興味深いのは、この平均値計算回路の結果のノイズ特性です。入力にOPアンプやADコンバータのようなアナログ回路を持ったデジタル・フィルター回路では、アナログ回路で発生する広帯域ノイズ(ホワイト・ノイズ)が信号に付加されます。移動平均では、サンプル値を幾つか足していくとその積算値になりますが、サンプル値に含まれるホワイト・ノイズは二乗で加算され、合計値はその平方根RSS(Root Sum Square)になります。例えばDCの値をサンプルした2個のサンプル・データを加算すると、信号値は2倍ですが、その各データに含まれるホワイト・ノイズは、二乗加算になるので、√2倍にしかならないということです。これはSN比の改善に役立つ特長です。サンプル数を2倍にすると、計算結果のSN比は約3dB(2÷√2)改善するということになります。
信号の平均値=(Sn+Sn−1+・・・Sn-m)/(m+1) Snは各アンプル値の信号
ノイズの平均値=(Vn2+Vn-12+・・・Vn-m1)−1 Vnは各サンプルのノイズ
sinc応答フィルターは、シグマデルタADコンバータ内で多用されていますが、実用的にはカスコードに何段かつないだsinc3〜sinc5などが使われています(3−5は段数)。
sinc3フィルターとsinc4フィルターの周波数特性を、図7に示します。図4と異なり縦軸が対数(dB)表示なっていることに注意してください。ノッチの周波数は、10Hz刻みです。sinc3では阻止帯域(ストップバンド)の盛り上がりは約1%(-40dB)に抑えられています。sinc4では-50dB以下になっています。ここまでくると、かなり実用的なローパス・フィルターといえます。
移動平均によるデジタル・フィルターは、より高度な応用回路がシグマデルタADコンバータの内部フィルターに使用されたりしていますが、統計や経済動向などにも多く利用されています。例えば過去7日間(一週間)毎の為替の動向であるとか、1カ月、3カ月、6カ月の工業生産の動向比較などです。短期やワンショットのデータではなく、トレンドを見たい場合によく使われます。
有限の過去データをフィルター計算に使用したフィルターがFIR型と呼ばれ、無限の過去のデータをフィルター計算に反映させるフィルターがIIR型となります。その方法を図にしたものが図8です。ここでは詳細については解説しませんが、そのデータ計算の流れを比較すると違いが分かります。図aのFIR型フィルターでは信号処理(計算)は1本のラインで、各ステップ(タップと呼びます)の計算結果は、最終結果への加算データとなります。計算はストレートに行われるので、動作が不安定になることはほとんどなく、誰が作ってもそれなりの結果が出ます。IIR型フィルターのバイクワッド・ブロックは、図bでみられるように一度出力されたデータが係数による処理を行われて入力側との加算に戻されています。これを回帰型アルゴリズムと呼びますが、電気回路的にはフィードバック回路のように見えます。フィードバック回路の注意点として、やり方を間違えると動作が不安定となり、時に発振を起こす可能性があるということです。これは計算で作るIIR型フィルターにも同じことが言えます。係数などの設計が不適切であると、このタイプのフィルターは不安定になることがあります。安定化の方法はアナログ・フィルターと同じで、ポール(極)に対してゼロを挿入して補正します。FIR型フィルターでは、ゼロができますがポールはできません。IIR型ではポールもゼロも作ることができます。この辺のところはより詳しい専門書を参照してください。
FIR型とIIR型フィルターはそれぞれ特長を持っていますが、どちらを使うかは、やはりアプリケーションのTPOになります。2つの実現方法の比較を表2に列挙しますので、参考にしてください。
今回のDown Load Contentsの中には、デジタル・フィルターの中で最も簡便な移動平均フィルター(sinc応答フィルター)が入っています。サンプリング間隔を考慮してうまく使用すると、高精度の測定を低ノイズで実行することができます。このデジタル。フィルターを生かすには、前半で述べたようにAD変換をする際のアナログ信号処理との効率的な組み合わせが、その性能に大きく影響します。デジタル処理を単なる計算と考えず、処理されているアナログ信号をイメージして設計すると最適な方法が見つかると思います。
次回のソリューションライブラリでは、より高度なフィルターの実現方法についてご紹介したいと思います。
Copyright © ITmedia, Inc. All Rights Reserved.
提供:ルネサス エレクトロニクス株式会社 / アナログ・デバイセズ株式会社
アイティメディア営業企画/制作:EDN Japan 編集部/掲載内容有効期限:2014年5月31日

2015年3月9日
津田建二の技術解説コラム【海外編】に知ってるつもりの外国事情(6)――IMECに見る研究開発のあり方を追加
2015年2月9日
津田建二の技術解説コラム【歴史編】に半導体の温故知新(6)――MOSトランジスタの次はTFET?を追加
2015年1月13日
津田建二の技術解説コラム【入門編】に半導体の基礎知識(6)――パワー半導体の広がりを追加
2014年12月8日
津田建二の技術解説コラム【海外編】に知ってるつもりの外国事情(5)――ネットワーキングを積極的に活用しようを追加
2014年11月10日
津田建二の技術解説コラム【歴史編】に半導体の温故知新(5)――ノーベル賞を受賞した半導体デバイスは実用的かを追加
2014年10月13日
津田建二の技術解説コラム【入門編】に半導体の基礎知識(5)――ワイヤレスに必要な半導体を追加
2014年10月6日
2014年9月8日
津田建二の技術解説コラム【海外編】に知ってるつもりの外国事情(4)――業界用語の常識を海外と比較するを追加
2014年9月1日
2014年8月11日
津田建二の技術解説コラム【歴史編】に半導体の温故知新(4)――IBM30億ドル投資の裏にCMOSの凄さありを追加
2014年7月28日
ソリューションライブラリ「デジタルフィルターとアナログフィルター(4):デジタル信号処理を徹底比較! フィルター特性と窓関数も解説」を追加
2014年7月14日
津田建二の技術解説コラム【入門編】に半導体の基礎知識(4)――IoTを定義しようを追加
2014年7月11日
Solution-Edge関連ニュースに信号の絶縁とAD変換が1つでできる便利な素子 AD7403を追加
2014年6月30日
ソリューションコラムにアナログ・デバイセズの実用回路集「Circuits from the Lab」の使い方を追加
2014年9月、ルネサス エレクトロニクスのイベント「DevCon Japan2014」にて、加賀デバイスブースにてソリューションエッジのインターポーザボード「SE SP-01」を使ったデータ・アクイジション・システムのデモが披露されました。今回は、このデモの詳細を加賀デバイスの開発担当者自らがご紹介します。
アナログ・デバイセズの実用回路集「Circuits from the Lab」を活用して、ルネサス エレクトロニクスのマイコン評価環境とつないで、お手軽、簡単データアクイジションシステムを構築してみましょう!
ソリューションコラムでは、これまでSE SP-01を使用したさまざまなバリエーションのデモをご紹介してきました。今回ご紹介するのは、アナログ・デバイセズの超低消費電力18ビット1Mサンプル/秒のA/DコンバータAD7982を、なんとGR-KURUMIを使用して制御&デバッグをします!
電子工作好きの皆さんにはおなじみの小型電子工作ボード(ガジェット)「GR-SAKURA」。このGR-SAKURAにセンサーを接続していろいろな装置作りにチャレンジしている方も多いと思います。そして、いろいろ工作しているうちに「もっと高精度なセンサーを使いたい」という欲求が生まれているかと思います。でも、高精度センサーをGR-SAKURAを接続するには、結構な技術力が要求されます。そこで、今回、Solution-Edgeオリジナルのインターポーザボード「SE SP-01」を使って、GR-SAKURに高精度センサーを手軽に取り付ける手順とプログラムをご紹介します。ぜひ、皆さんもSE SP-01でGR-SAKURAを究極まで進化させてください。
前回のソリューションコラムでは、SE SP-01を使って手軽にシステム構築ができる一例を紹介しました。今回は、前回に組み上げた評価環境を実際に動作させていく様子をご紹介します。SE SP-01の素晴らしさを、よりご理解頂けると思います。
アナログ・デバイセズ製の各種デバイスと、ルネサスエレクトロニクス製マイコンボードを簡単につなぐことができるようになるインターポーザボード「SE SP-01」。実際どれくらい簡単なのでしょうか。早速、SE SP-01を使ってシステムを組んでみましょう。
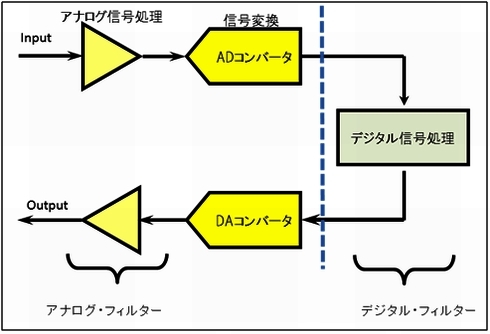 【図1】アナログ入出力信号処理の流れ
【図1】アナログ入出力信号処理の流れ 【表1】デジタル・フィルターとアナログ・フィルターの比較
【表1】デジタル・フィルターとアナログ・フィルターの比較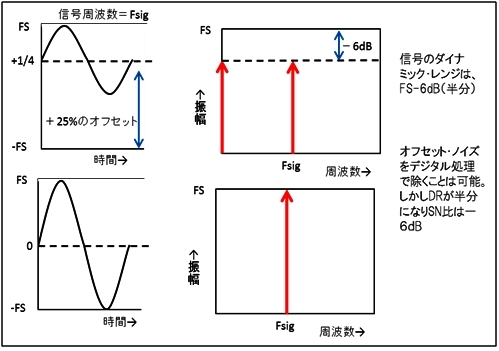 【図2】大きなオフセットノイズの除去
【図2】大きなオフセットノイズの除去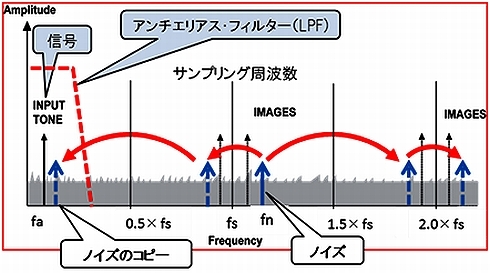 【図3】折り返しによるコピー
【図3】折り返しによるコピー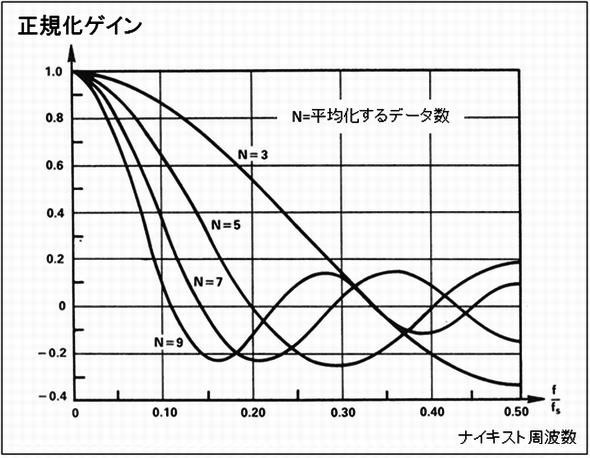 【図4】移動平均フィルターの正規化周波数応答
【図4】移動平均フィルターの正規化周波数応答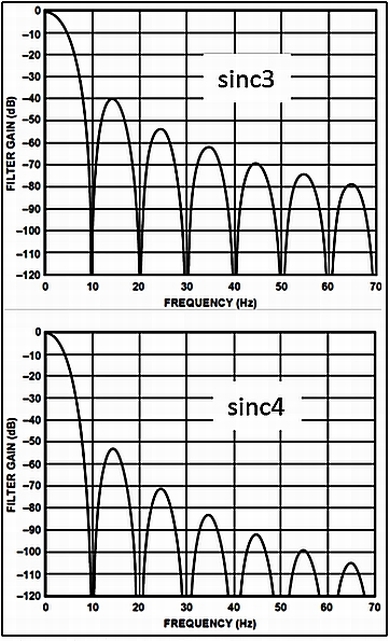 【図7】sinc3とsinc4フィルターの応答
【図7】sinc3とsinc4フィルターの応答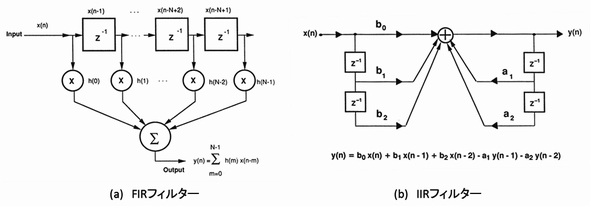
 【表2】FIRフィルターとIIRフィルターの比較
【表2】FIRフィルターとIIRフィルターの比較







