Spiceの新しい応用解析:自然対流問題(その1):SPICEの仕組みとその活用設計(19)(1/3 ページ)
Spiceが持っている解析能力について基本的な動作とその注意点について説明してきた本連載。今回からは、Spice関連セミナーなどでは、紹介されることの少ない応用解析について説明していきます。
本連載では切り口を変えながらSpiceが持っている解析能力について基本的な動作とその注意点について説明してきましたが、今回からはセミナーなどで紹介される内容と少し趣向を変えて、従来のセミナーでは紹介されないSpiceの応用解析について説明していきます。
CFDツールの課題とSpiceによる自然対流解析
本連載がスタートした当初の3回目の巻末コラムに次のような記事を書きました。
ここでのお約束通り、通常の解析であればCFDツールでなければ解けない自然対流問題についてSpiceを適用した事例を今回から数回にわたって紹介します。
SPICEを有限要素法/有限体積法と比較する
これらの比較から、「ヤング率が高い(=硬い)材料は材料の変形が少ない」ということは、「電気伝導率が高い材料(金属など)は抵抗値が小さいため電位差が発生しにくい」ことに相当します。熱流体解析の熱伝導率と温度差の関係も同様です(「理想材料を使えばロスが出ない」ということです)。
多くの有限要素法のツールがオプションとして熱伝導モードを持っているのは、このように簡単に対応が取れるからなのです。ですから、うまく材料定数や境界条件を設定すれば、プリント基板の電位分布を有限要素法の熱伝導モードや熱流体解析ツールの2次元モードで求めることができます。
逆に言うと、熱の問題をSPICEで解くことも、条件や工夫しだいで可能になるわけです。詳細については本連載の最終回で取り上げる予定です。
解析環境の充実にしたがって、最近では電子回路の開発・設計の多くの場面で回路シミュレータが用いられるようになってきていますが、その中で例えばスイッチング電源で生じた損失(=熱)をどのように放熱するかについての論議はあまり見かけることはありません。
このような熱問題に関してはまだまだ専用のCFD*1)ツールが用いられているのが実態なのですが、CFDツールの年間レンタル料金は数百万円/年程度が相場であり、回路解析に対して熱解析は解析コストが桁違いに高い点が導入に当っての障害になります。
*1)CFD
流体問題を解く一般的な手法は、運動量保存則から導かれるナビエ・ストークス方程式と、質量保存則(連続の式)、その他の保存則を基に、種々の仮定をおいて得られる式を解くことで得られますが、一般解はまだ見つかっていません。現実的には対象空間をいくつかの細かい空間に区切って、微分方程式を代数方程式に置き換える数値解法が用いられており、この計算手法をComputer Fluid Dynamics(CFD)と言います。
連続的な微分方程式を限られた数の代数方程式に置き換えるため、この置き換えの割り当て方で近似精度に差が出てしまいます。ちなみに対象領域を細かい空間に置き換えることを「メッシュを切る」、あるいは単に「メッシング」と言い、解析者の経験によるノウハウの重要な部分です。
また、静音性が問題視されるAV機器では自然対流で放熱するのが一般的なのですが、自然対流問題ではその対流を起こす力の源が微弱なため、空気の粘性によるメッシュの依存性を強く受け、解析者の技術レベルによって結果が大きく変わってしまいます。そのようなメッシュ依存性の例を図1に示します。
CFDツールを使っても経験と知識がないと自然対流問題はうまく解けないのです。
熱抵抗回路網法とは
任意直方体内の熱の流れにくさの指数である熱抵抗Rthは、物体の物性値である熱伝導率λを使って、
で表されます。
(熱伝導率λとは単位立方体の対面に1Kの温度差を生じさせる熱流量で、単位は「W/(m・K)」です)
この式は電流の流れにくさの指数である電気抵抗Rの
という式に形式的に一致しています。
また、熱に関する「フーリエの法則」から、温度差(ΔT)、熱流量(W)、熱抵抗(Rth)の3者は次のように関連付けられています。(−記号はΔXとΔTの極性調整用)
| E(電位差) | ↔ | ΔT(温度差) |
|---|---|---|
| I(電流) | ↔ | Q(熱流量) |
| R(電気抵抗) | ↔ | Rth(熱抵抗) |
| 表1 回路と熱のパラメータの対応 | ||
これらから、電気と熱のそれぞれの因子は表1のように対応していることが分ります。
つまり、E=I×Rの式で熱問題を解くことができるわけです。
この関係を使って、熱の流れを表す回路網を電気的に実現し、これを解くことで温度分布を求めようとする手法が熱抵抗回路網法なのです。
次回、実用例として説明しますが適用可能な形状では極めて高速・高精度に答えを求めることができます。
Copyright © ITmedia, Inc. All Rights Reserved.
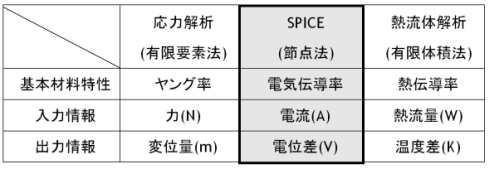 表A 数値解析手法と入出力情報
表A 数値解析手法と入出力情報 図1 メッシュ依存性 (参考資料1-図5から引用)
図1 メッシュ依存性 (参考資料1-図5から引用)





