ダイオードなどの非線形負荷を節点法で解析する:SPICEの仕組みとその活用設計(3)(1/3 ページ)
電圧と電流が比例する線形負荷と異なり、電圧と電流が比例しないダイオードのような非線形負荷も存在する。第3回は、SPICEの節点法における非線形負荷の解析手法について説明する。
前回は、SPICEに用いられる節点法について、以下の3つの手順を説明させていただきました。
- 回路要素行列[G]の作り方
- 電流ベクトルの作り方
- 行列[G]の逆行列を電流ベクトル[I]に掛けて電圧ベクトル[V]を求める方法
これらの手順についてはご理解いただけたでしょうか? また、慣れ親しんだ「抵抗」に代わるものとして取り上げた「コンダクタンス」についてはイメージできたでしょうか?
「多くの手法を習得するのは困難だ」と思われるかもしれませんが、1つの解析手法をマスターすれば、他のものの習得は標準語に方言を足していくようなものです。最終ページに掲載したコラム記事も参考にしてください。
それでは今回は、非線形解析について取り上げたいと思います。
非線形解析とNewton-Raphson法
前回までは電圧と電流が比例する線形負荷を考えてきましたが、今回はダイオードに代表される非線形負荷を考えます。
ダイオードの基本的な電圧/電流の関係式は、式(1)のショックレーのダイオード方程式として表されます。
ここで、Ifはダイオード順方向電流、Vfは順方向電圧、Isは逆漏れ電流、Kbはボルツマン定数、Tは温度(K)、qeは電子の素電荷量です。
この負荷は非線形素子の代表的なもので、Vfを変えた場合、Ifはリニアに変化しません。従って、コンダクタンスが定数でない以上、機械的に回路要素行列[G]を組み立てることができないのです。
このような場合の方程式の根を求める求根法はいろいろな手法が存在しますが、今回は収束が早く、アルゴリズムが明確な「Newton-Raphson法」で近似解を求める手法を取り上げます。
「Newton-Raphson法」と動作点
一般的にNewton-Raphson法は、図1のように「f(X)=0になるXを求める」という形で表記されることが多いのですが、電子回路においてf(X)=0が何を意味しているのか、イメージをつかめる人は少ないと思います。
まず、非線形解析の前段階として、図2のような電圧源V0と内部抵抗R0からなる回路に、外部抵抗RXをつないだ場合のRXに掛かる電圧・電流(Vx、Ix)特性の様子を考えます。
RXの値は不明ですが、必ず0Ωから∞の範囲に入っているはずであり、その場合、VxとIxの関係は式(2)で示されます。
式(2)から、
- IX=0、つまり開放時はVX=V0
- VX=0、つまり短絡時はIX=G0×V0=I0
と計算でき、これらの関係を図で示せば、図3のようにI0とV0を結ぶ直線となります。この直線を負荷線と言います。
非線形負荷といえども、線形負荷と同じく、電圧を印加すれば電流が流れます。ですから、図2において、非線形負荷RXに電圧が印加されて負荷電流IXが流れたとき、内部抵抗R0にはIXに対応した電圧降下を生じ、Rxの両端電圧VXは図3の負荷線上をV0から(Vx、Ix)なる交点まで移動して安定することになります。
結局、非線形解析とは、この負荷線と非線形負荷の交点を求めることなのです。この交点を動作点と言います。
Copyright © ITmedia, Inc. All Rights Reserved.
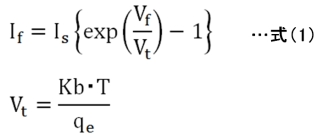
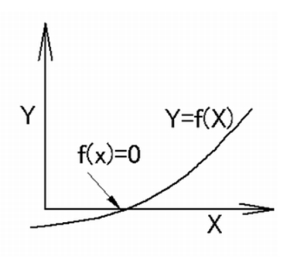 図1 Y=f(X)の曲線
図1 Y=f(X)の曲線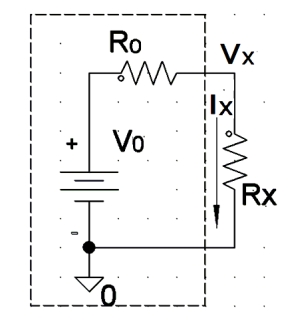 図2 検討回路
図2 検討回路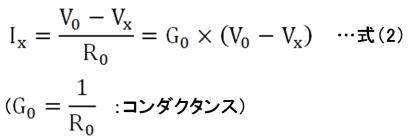
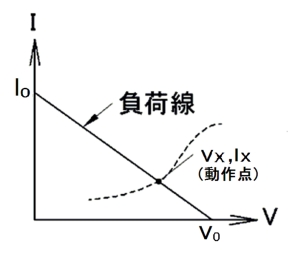 図3 負荷線
図3 負荷線


