ダイオードなどの非線形負荷を節点法で解析する:SPICEの仕組みとその活用設計(3)(3/3 ページ)
ダイオード電圧の計算例
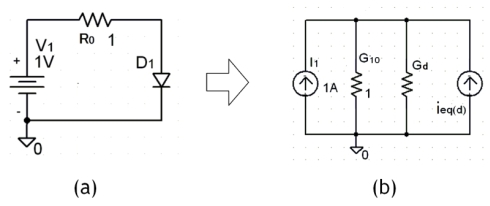
例として図9(a)のように、ダイオードに抵抗R0(1Ω)を介してV1から1Vの電圧を与えた場合のダイオードの順方向電圧を求めてみます。
この回路の解を求める方程式は式(6)であり、expの項とその外部に順方向電圧Vfが存在するために一般解を求めることはできません。
今回の手順に従って、まずV1とR0の電圧源をI1とG10の電流源に変換し(ノートンの定理)、図8に示したダイオードの等価回路と組み合わせれば、全体の回路構成は図9(b)のようになります。
この回路の等価コンダクタンスGと補正電流Ieq(d)は式(7)で計算できます。
一方、対応する電流ベクトル[I]は図9(b)から、式(8)となります。
図9(b)の回路は節点が1と0の2つしかありませんから、回路要素行列[G]は1行1列になり、次計算サイクルの順方向電圧Vfi+1は節点1、0間の電圧V1になります。つまり、式(9)で求めることができます。
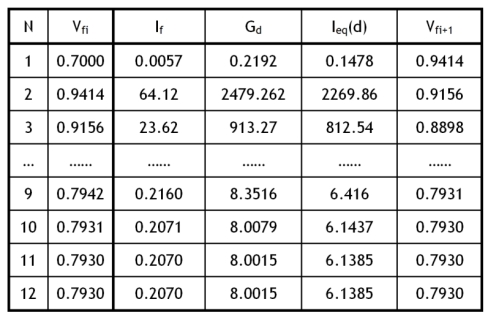
Isとして10−14A(1Aクラスのダイオード相当)、Vfとして0.7Vを与えたときの計算結果を表1に示します。
Ta=27℃近辺ではVt=Kb・T/qe=25.86mV程度ですから、
といったように、次サイクルの計算に必要な値が求まります。続いて、2回目のVfiとして新しく0.9414Vを代入して繰り返して計算していくと、表1のようにVfiは12回目ぐらいで0.793V近傍へ収束します。
なお、接線コンダクタンスGd、補正電流Ieq(d)は計算サイクルのたびに変化するので、回路要素行列[G]、電流ベクトル[I]も毎サイクル更新することになります。
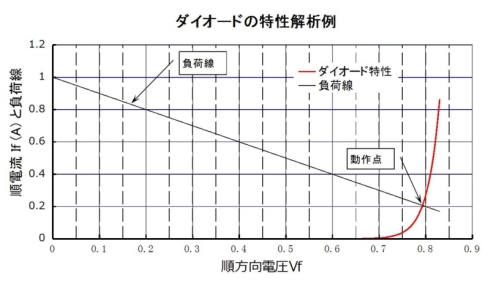
別の手法としての図式解法の結果を図10に示しますが、交点は0.79V前後ですから今回の手法の妥当性が分かります。
次回は、SPICE解析の要である電圧や電流が時間的に変化する過度解析について説明します。
SPICEを有限要素法/有限体積法と比較する
節点法の理解を助けるために、SPICEで使うパラメータを、有限要素法や有限体積法と対比してみましょう。
電気回路で使う抵抗値は構造的には次のように計算されます。
この抵抗値Rに電流Iを流した場合の電位差ΔVはオームの法則に従って
となります。
一方、材料力学で扱う変位ΔLは、ヤング率を使って求められます。
この式を変位ΔLについて解くと次の結果を得られます。
2つの式を比較すると、
電位差ΔV⇔変位ΔL 電流⇔力 電気伝導率⇔ヤング率
がそれぞれ対応していることが分かります。実際、1次元のバネ問題はSPICEで解くことが可能です。
表Aによく使われる数値解析手法との対比をまとめておきます。
これらの比較から、「ヤング率が高い(=硬い)材料は材料の変形が少ない」ということは、「電気伝導率が高い材料(金属など)は抵抗値が小さいため電位差が発生しにくい」ことに相当します。熱流体解析の熱伝導率と温度差の関係も同様です(「理想材料を使えばロスが出ない」ということです)。
多くの有限要素法のツールがオプションとして熱伝導モードを持っているのは、このように簡単に対応が取れるからなのです。ですから、うまく材料定数や境界条件を設定すれば、プリント基板の電位分布を有限要素法の熱伝導モードや熱流体解析ツールの2次元モードで求めることができます。
逆に言うと、熱の問題をSPICEで解くことも、条件や工夫しだいで可能になるわけです。詳細については本連載の最終回で取り上げる予定です。
執筆者プロフィール
加藤 博二(かとう ひろじ)
1951年生まれ。1972年に松下電器産業(現パナソニック)に入社し、電子部品の市場品質担当を経た後、電源装置の開発・設計業務を担当。1979年からSPICEを独力で習得し、後日その経験を生かして、SPICE、有限要素法、熱流体解析ツールなどの数値解析ツールを活用した電源装置の設計手法の開発・導入に従事した。現在は、CAEコンサルタントSifoenのプロジェクト代表として、NPO法人「CAE懇話会」の解析塾のSPICEコースを担当するとともに、Webサイト「Sifoen」において、在職中の経験を基に、電子部品の構造とその使用方法、SPICE用モデルのモデリング手法、電源装置の設計手法、熱設計入門、有限要素法のキーポイントなどを、“分かって設計する”シリーズとして公開している。
関連記事
- >>SPICEの仕組みとその活用設計
 節点法の計算原理を例題から学ぶ
節点法の計算原理を例題から学ぶ
第2回は、簡単な例題回路を使って節点法の計算を実際に行う。節点法の計算原理を理解するためにも一度は手計算で解いてみよう。 SPICEの内側を探る――節点法とは
SPICEの内側を探る――節点法とは
電子回路を設計する上で必須となっているSPICE。本連載では、そのSPICEの仕組みと活用法を取り上げる。第1回は、SPICEを使う目的や、数多く存在するSPICEツールの選定基準、SPICEの解析手法である節点法について説明する。
Copyright © ITmedia, Inc. All Rights Reserved.
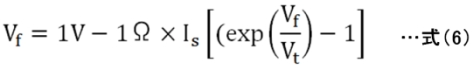
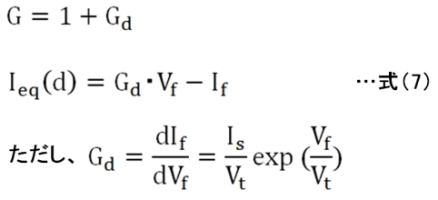
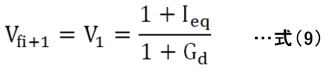
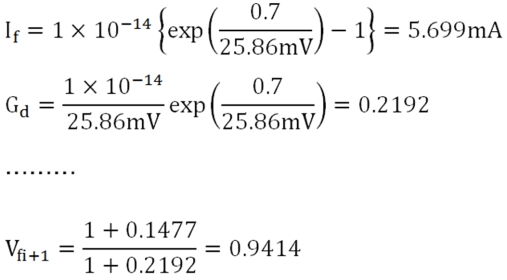


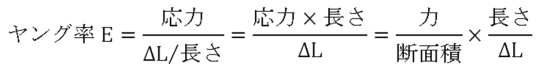

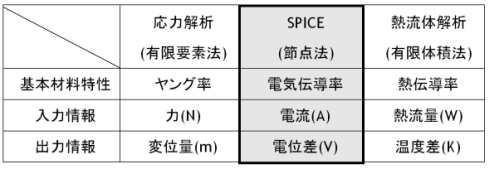 表A 数値解析手法と入出力情報
表A 数値解析手法と入出力情報


