信号発生器を選ぶ、使う:何年たっても変わらないその秘訣(2/3 ページ)
選択が困難な理由
信号発生器のアーキテクチャには長所と短所がある。それぞれを理解した上で、その特性がある特定の作業に適しているのか、それともその用途には別のモデルを選択すべきなのかということを見定める必要がある(表2)。理解が不十分であると、性能上の問題で、その製品を使用するのが不適切であることに気づくまでに時間がかかってしまうかもしれない。
信号発生器製品を評価するのは、意外に複雑な作業である。その複雑さの原因になっているのは、メーカーによってAWGなどの用語の使い方が一貫していないことだ。多くのSFGは、正弦波、方形波、のこぎり波、三角波といった標準的な波形を生成するのには適しているが、任意波形は制限付きでしか生成できない。
SFGに任意波形の生成機能を追加するのはそれほどコストがかかることではない。また、ユーザーもいつの日か任意波形の生成が必要になるかもしれないと考え、その機能が付加されている製品に魅力を感じる。しかし残念なことに、メーカーはしばしばSFGのことを、ARBあるいはAWGと呼んでいることがある。SFGは、一般的にはより高価な、真のARBに匹敵する任意波形生成機能を持っていないのにもかかわらずである。また、基本的にはSFGだが、限られた任意波形生成機能を持つものに対し、「AFG」(arbitrary function generator:任意ファンクションジェネレータ)という言葉を使用するメーカーもある。
さらに製品の選択を難しくしているのは、真のAWGの多くがDDSを用いて掃引(スイープ)周波数クロックを生成しているという事実である。DDSは掃引周波数の生成に最適であり、また多くのSFGにおいて掃引機能は重要な特性でもある。しかしながら、掃引周波数クロックの生成にDDSを用いるAWGが、必ずしもAWGとSFGの特性の最高の組み合わせを提供しているわけではないのだ。
SFGの特徴
信号発生器のアーキテクチャは、上述した通り、SFGとAWGに分けることができる。ここでは、SFGについてより詳細な解説を行う。
位相アキュムレータ
SFGで最も重要な要素は位相アキュムレータ(位相蓄積機能)である(図5)。この高度な機能ブロックは、固定周波数fCの基準クロックを、安定した低い周波数fOの出力クロックに変換する。fOとしては、広範囲の値を高い精度で設定可能である。周波数の変更を小さいステップ、大きいステップで行うこともできるし、ステップ間での瞬時な変更も可能だ。また、周波数が変化する際、出力信号の位相が保たれる点にも特徴がある。つまり、10MHzの信号を出力していた際、信号周期の227°のポイントで周波数を100kHzに変更したとすると、100kHzの信号波形は227°のポイントから始まる。さらに、位相アキュムレータがアナログ出力信号を生成するD-Aコンバータを駆動している場合、出力振幅に不連続性が生じない。出力信号が正弦波などの連続波形である場合は、その傾きが変わるだけなのである。
位相アキュムレータでは、2進数Mを指定することで、ある特定の出力周波数fOを生成するという方法をとる。そのため、位相アキュムレータを用いたDDSは掃引周波数の生成に最適である(Mが2進化10進数形式の実装も存在する)。Mの値が大きいほどfOは高くなり、Mの値を連続的に変化させるとfOも連続的に変化する。時間の経過に伴って適切に変化する値をMとして指定することで、あらゆる種類の掃引パターンを無限に生成することが可能なのだ。生成する信号として一般的なのは、線形/対数ランプ波、のこぎり波、周波数が変化する正弦波であろう。
この方法では、出力周期を2Nの間隔(またはステップ)で分割すると考えることができる。N=14とすると、2N=16384となり、各ステップは360°/16384、つまり0.02197°となる。N=14でM=2048の場合、サンプル点は45°間隔となり、fO=fC/8となる。M=1ならサンプル点は0.02197°間隔であり、fO=2−14 ×fCである。
この例ではMを2の累乗の数としているが、実際のシステムはこれよりも複雑であり、Mは14ビットの2進数で、1から16384までの整数値をとる。しかし、出力周期は正確にサンプル周期の整数倍でなくてもよい。このように要件が厳格でないことから、SFGは高い周波数分解能を実現することができる。つまり、fOを非常に小さな値で調整することが可能なのだ。
なお、SFGはサンプルデータシステムであるため、サンプリング定義の制約を受ける。上述した例であれば、理論的な最大出力周波数は0.5×fC未満となる(実際には、さらにそれより低く、約0.4×fC程度だ)。
その他の機能ブロック
SFGの重要な要素の1つが位相アキュムレータであることは確かだが、それがすべてというわけではない。所望の信号を得るには、掃引/可変の周波数信号をアナログ波形に変換する必要がある。この変換には、波形データを格納するメモリー(以下、波形メモリー)、D-Aコンバータ、出力信号のコンディショニング(整形)機能が必要となる。コンディショニング機能としては、D-Aコンバータ出力のフィルタリングが必須であり、出力のデグリッチングや増幅機能も必要な場合が多い。方形波は生成が容易なので例外であることが多いが、標準的な波形を定義するデータ集合は、ROMベースのルックアップテーブルに格納される。ROMにデータ集合を置くことで立ち上がり/降下時のスルーレートの正確な制御が可能になるため、方形波のデータ集合もROMに格納する場合がある。一方、ユーザー定義、つまり任意波形用のルックアップテーブルは、ROMではなくRAMで実現する。
fOが高い場合、波形を定義するデータのポイント数は少なくなる。つまりfOが増加すると、ルックアップテーブルの値のうち、D-Aコンバータに送られずスキップされるデータの数が増える。逆にfOが小さい場合には、データ集合の次の値に移る前に、ルックアップテーブルのある値、またはすべての値が繰り返しD-Aコンバータに送られることもある。
直観的には分かりづらいかもしれないが、多くのSFGは単一周波数のクロックを使用して入力データを周波数シンセサイザに送っており、コーナー周波数が出力信号の繰り返しレートに依存する出力ローパスフィルタを必要としない。比較的簡単な固定周波数の出力フィルタを使用できることが、SFGのコスト効率を高めている主な理由である。
SFGは非常に魅力的な特性を多く備えているが、もちろん完璧というわけではない。例えば、fOの値が大きい場合には、波形定義に用いるルックアップテーブルのデータがスキップされている可能性があり、逆にfOの値が小さい場合には、同じ点を繰り返しているかもしれない。
また、fOを決定するMは、ルックアップテーブルの容量の約数でなくてもよい。そのため、周期ごとに波形に違いが生じる。つまり、出力波形の連続する繰り返しにおいて、各々の波形はルックアップテーブルの異なるデータを使用して生成されたものである可能性があるということだ。このため、SFGの出力は、周波数軸で見れば非常に安定した平均値を持つが、時間軸で見ると周期ごとに波形に違いがあり、用途によっては、そのことが問題となる可能性がある。
また、代表的な波形のためのメモリー容量は214(16384)ポイントで、十分かもしれないが、ユーザー定義の任意波形では16Mポイントものデータが必要となることも多い。さらにユーザーは、条件分岐やループを用いて波形セグメントを繰り返すことで、効率的に波形を生成したいと思うかもしれない。信号発生器において、条件分岐とは、ある条件を満たす場合に波形定義テーブルの指定された点へと移動する機能のことを意味する。一方、ループは、ある範囲の波形定義点を、指定された回数、またはある条件を満たすまで繰り返す機能のことである。このような機能はAWGでは一般的だが、現在市場に出回っているSFGでこれらの機能を持つものはない。
Copyright © ITmedia, Inc. All Rights Reserved.
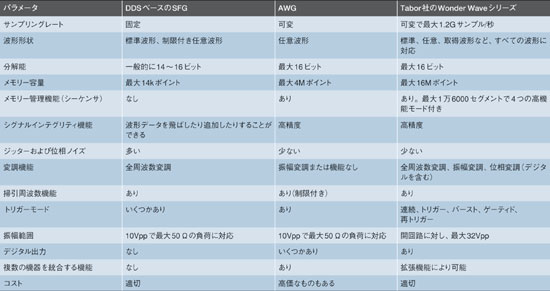
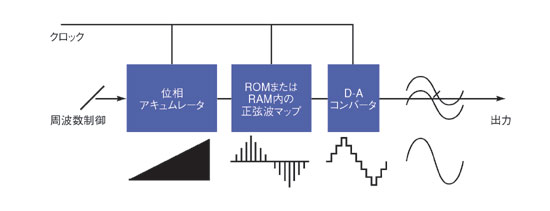 図5 位相アキュムレータを利用した信号発生器 掃引周波数機能を持つSFGおよびほとんどのAWGが、位相アキュムレータ(DDS技術をベースとしたクロック発生器)を使用している。
図5 位相アキュムレータを利用した信号発生器 掃引周波数機能を持つSFGおよびほとんどのAWGが、位相アキュムレータ(DDS技術をベースとしたクロック発生器)を使用している。


