実は足し算しかできない!? 「補数」「シフト」で四則演算しているマイコン:マイコン入門!! 必携用語集(5)(1/2 ページ)
皆さんご存じのように、マイコンはいろいろな演算を行います。でも、実は算術演算の中では足し算しかできないんです。マイコンは足し算と、論理反転とシフトを組み合わせて、その他の算術演算(引き算、掛け算、割り算)を実現しています。では、どうやって演算しているのかを説明します。
加算(足し算)
最初に最も簡単な加算(足し算)を説明します。
これは10進数と同じ方法で計算します。各桁が加算した後に2になる場合は「桁上がり」が発生し、1桁上の数字に加算します。図1に2進数の[0110]*)と[0011]の加算例を示します。
*)本文中では、便宜上、2進数の値を[0]や[1]のように、[ ]で表現します
ちなみに、上がった桁のことをキャリー(Carry)と呼びます。逆に上の桁から1を借りてくることをボロウ(Borrow)といいます。よく使いますので覚えておいてください。
減算(引き算)
次に減算(引き算)を説明します。前述したようにマイコンでは直接減算(引き算)を行えません。そこで補数を加えて間接的に減算を行います。
では、補数とは何でしょうか?
補数とは、「その数字に足した時に、桁上がりが起きる数のうち最も小さい数」です。
10進数の場合、足して10になる数字、2進数なら2([10])になる数字です。
10進数の場合、足して10になる数を「10の補数」といいます。2進数の場合、足して2になる数字を「2の補数」といいます。
以下に例を挙げます。
10進数の場合
6の「10の補数」は4です。3の「10の補数」は7です
2進数の場合
[1]の「2の補数」は[1]です
([1]+[1]=[10]:桁が上がります)
そして、[1101]の「2の補数」は[0011]になります
([1101]+[0011]=[10000]:桁が上がります)
では、補数を足してみましょう。どんなことが起こるでしょうか?
まずは理解しやすいように10進数でやってみましょう。
9から6を引く場合
9に、6の補数である4を足してみます
9+4=13
この時、上がった桁を無視して、1桁だけみると……3。
9−6=3の答え「3」と同じになりました!
実は、補数を足して上位の1桁を無視することで、引き算ができるのです。
次に2進数の場合を見てみましょう。
[1111](15)から[1101](13)を引く場合
[1101]の補数は[0011]でしたから、[1111](15)に[0011](3)を足します
[1111](15)+[0011](3)=[10010](18)
この場合も上がった桁は無視して、下4桁だけみると[0010](2)になります
[1111](15)−[0011](13)=[0010](2)の答え[0010](2)と同じです!
こちらも補数を足すことで、引き算ができました。
このように補数と加算(足し算)で、引き算を行うことができます。でも補数を作る計算をしなくてはなりません。
実は、マイコンでは簡単に2([10])の補数が作れます。それは、各桁を反転([0]なら[1]、[1]なら[0]に)して、最後に[1]を足せばいいのです。図2を見てください、[1101]の各桁を反転させ[0010]にして、[1]を足せば補数の[0011]ができることが分かると思います。各桁の反転は論理演算の反転回路(インバータ)を使うと簡単にできます。[1]を加える加算回路はインクリメンタと呼ばれ、簡単な加算回路で実現できます。
もう1つ補数を作る方法があります。上位の桁から[1]と[0]を反転していき、最後の[1]以降は反転しないでそのまま使います。例えば[1101]は上位の[110]は反転して、最後の[1]は反転しないと[0011]になります。[1010]は上位の[10]は反転して[01]にしますが最後の[1]以降の[10]は反転しないでそのまま使いますと[0110]となって補数になります。ただし、この方法は「どれが最後の[1]か」を見分けるのがマイコンには難しくなるため、一般的には全ての桁(=全ビット)を反転して[1]を加える方式を使っています。
Copyright © ITmedia, Inc. All Rights Reserved.
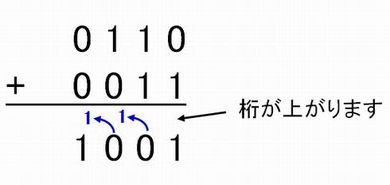 【図1】2進数の加算
【図1】2進数の加算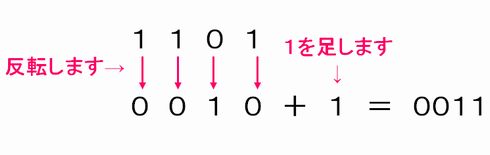 【図2】2進数の補数の作り方
【図2】2進数の補数の作り方


