ラプラス素子(その2):SPICEの仕組みとその活用設計(24)(1/4 ページ)
ラプラス素子はSpiceツールベンダー各社の独自拡張機能であり、ツール毎に振る舞いも多少異なります。そこで、今回はV&Vの観点で各ツールのラプラス素子の振る舞いについて見ていきます。
前回は過渡現象問題を解く時に必須となるラプラス変換・逆変換をSpice上で行うラプラス素子について概要を説明しましたが、このラプラス素子はツールベンダー各社が独自に追加した拡張機能です。したがってその機能の実装手法に統一性がなく、ツール毎に振る舞いも多少異なっています。今回はV&Vの観点で各Spiceのラプラス素子の振る舞いについて見ていきます。
畳み込み積分の精度検証
畳み込み積分の概要については前回説明しましたので、ここでは畳み込み積分の基礎になるインパルス応答について考えます。
例題の回路は図1に示すように回路の周波数特性を変数Sで表現した伝達関数T(S)として定義されています。
インパルス応答波形とはこのような伝達関数T(S)で表される回路にインパルス波形を印加した時の出力波形であり、インパルス波形をラプラス変換したものは1ですから伝達関数T(S)自身がインパルス応答波形を表していることになります。
ここで問題となるのはインパルス応答を含む過渡応答は時間領域の波形であり、図1の回路は基本的には周波数領域の特性であるという点です。
この周波数領域から時間領域への変換を人の手で行うのならラプラス逆変換表が使えるのですが、この手法は機械的ではありません。もっと機械的に変換できる方法はないのでしょうか?
ここでラプラス変換の基礎になったフーリエ変換を考えてみましょう。
フーリエ変換は対象となる波形を周波数成分に分解します。逆に言えばこれらの周波数成分を合成すれば元の波形を表現できるということです。
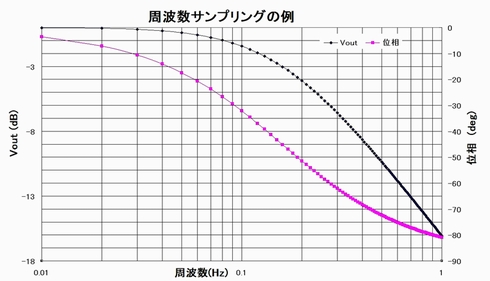
したがってS→jωに置き換えて一定周波数間隔でサンプリングを行い(図2のマーカー点)、各周波数の出力振幅と位相を合成すれば伝達関数、すなわちインパルス応答波形を求めることができます。
Copyright © ITmedia, Inc. All Rights Reserved.
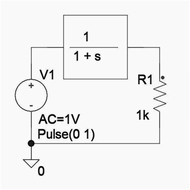 図1 検討回路例
図1 検討回路例