SW電源の解析：SPICEの仕組みとその活用設計（最終回）（3/4 ページ）

[加藤博二（Sifoen），EDN Japan]

その他測定手法の補足説明

　比較検討の対象としたその他の測定法について簡単に説明します。

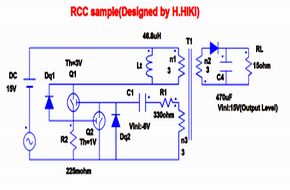
　なお、状態平均化法は周期が一定でないと使えませんのでRCCのように周波数が変化するタイプのコンバータには状態平均化法では解析できません。RCCの結果は測定値のみです。

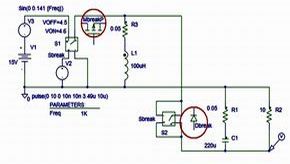
• SpiceｰFRA法：Spice上に構成したコンバータ回路の制御系に変調信号を注入し、周波数を可変しながら出力電圧に現れる信号成分を測定します。精度を上げるためには変調周波数の刻みを細かくする必要があり、加えて安定状態の判定を各周波数で確認する必要がありますので時間と人手がかかります。
• SCAT-FRA法：SCATはSW電源の解析用に開発されたシミュレーションツールで、Spice-FRAと同じ原理によるFRA特性の測定機能を備えています。安定状態の収束判定も自動で行います。(所用時間は計測不可)
• 状態平均化法：状態平均化法とはスイッチがON状態および、OFF状態の微分方程式をそれぞれ算出して通電時比率を考慮した定常状態を導くものです。「スイッチングコンバータの基礎」コロナ社1999/8/20発行初版第4刷を基に算出しています。

検討結果

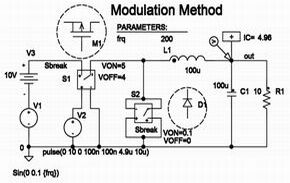
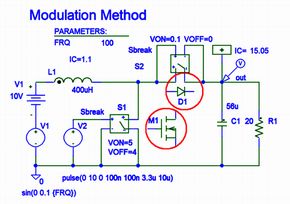
　比較対象として、電流連続モードの、降圧コンバータ(D=0.5)、昇圧コンバータ(D=0.333)、反転コンバータ(D=0.5)、RCC(D=0.5)の解析結果を表1に比較します。(D:通電時比率)なお、表1では各手法の精度比較という目的のため、各コンバータの入力電圧を変動させて基本伝達特性のみを比較しています。
(時比率Dや負荷抵抗RLを変動させると余分な周波数特性が付加されてしまいます)

降圧コンバータ(δ=0.5) （クリックで拡大）

昇圧コンバータ(δ=0.333) （クリックで拡大）

反転コンバータ(δ＝0.5) （クリックで拡大）

RCC(δ=0.5) （クリックで拡大）

表1：各種コンバータの解析手法比較

コンバータタイプ		高← ピーク値捕捉順 →低
降圧コンバータ		状態平均化法	Step応答法	Spice-FRA	SCAT-FRA
昇圧コンバータ		状態平均化法	Step応答法	Spice-FRA	SCAT-FRA
反転コンバータ		状態平均化法	SCAT-FRA	Step応答法	Spice-FRA
表2：ピーク値捕捉状態比較

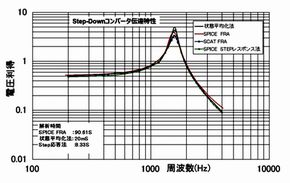
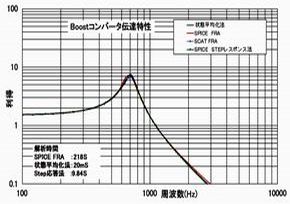
　表1の検討結果から、RCCを除く3コンバータ方式は2次遅れ系の特性を持つこと、そしてどの解析手法を用いても結果に大差がないことが分かります。ですから理論解が明快な状態平均化法を用いれば変曲点や共振峰を構成する部品定数、影響度などを算出でき、的確に検討を進めることができます。

　例えば、状態平均化法によれば、降圧コンバータは通電時比率Dに周波数特性が無く安定性が高いことが分かりますし、昇圧型や反転型では通電時比率Dの特性に前回説明した(1-S)特性が現れることに加えてDの非線形の影響を強く受けることが分かります。また、基本的に制御系を安定にしたければ共振のピークを下げるためにL→大、C→小の方向へ検討を進めなければならないことも分かるのです。

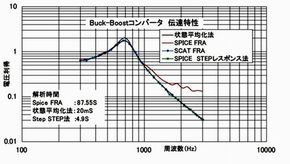
　精度の観点から表2の結果を見れば系のピークを正確に補足しているのは状態平均化法ですが、Step応答法も安定してピークを捕捉しています。一方、これまで使われている手法を模擬した2つのFRA法では周波数刻みをどのように設定するか？がキーポイントになり、うまくピーク値と設定周波数が合致するように粗解析→詳細解析を行う必要があります。

　また、RCCについては2つのFRA法とStep応答法は概略合致していて1次遅れ系であることを示し、経験的な安定性の高さを裏付けています。
(高周波域での振動はSpiceモデルの完成度の低さによるものです)