マイコンアーキテクチャの基本理解 〜 キャッシュ構成、エンディアン、浮動小数点、バス構成、例外処理:ハイレベルマイコン講座:【アーキテクチャ概論】(2)(2/3 ページ)
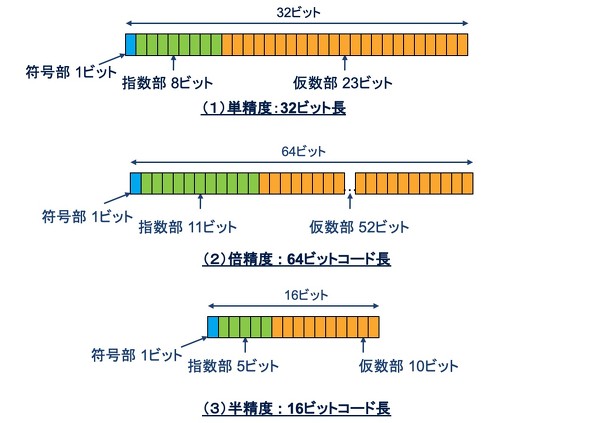
浮動小数点演算
32ビットマイコンが1度に扱えるデータは232=4294967296だ。これ以上大きいデータを扱う場合や、小数点を扱う場合は、5.0×1012(5.0e12)のような浮動少数点演算が必要になる。ソフトウェアでも、浮動小数点演算は可能だが、固定小数点に移行するためのスケーリング処理と、飽和に関する問題のハンドリングのため、アルゴリズムの作り替えと固定小数点の実装が必要となり、かなり複雑なプログラムになる。浮動小数点演算が必要な用途は、例えば、自動車分野であれば、パワートレイン、ABS、トラクション制御などである。また、デジタル家電や、ゲームなどの3D画像処理、レーザープリンタ、デジタルカメラなどのイメージ処理で使用される。産業機器分野では電源制御などに使われ、一般的に高機能なアプリケーションでの必須機能になっている。
浮動小数点演算には、半精度、単精度、倍精度などの性能がある(図3参照)。一方、浮動小数点規格は、一般的に2008年8月に制定されたIEEE 754-2008に準拠するが、この規格に完全に準拠してるかどうかが性能チェックのポイントになる。どのような浮動小数点機能が実装されているのかも、アーキテクチャの一部と考えられる。
浮動小数点演算については、「Q&Aで学ぶマイコン講座(17):浮動小数点演算のメリット」で詳しく解説している。
バス構成
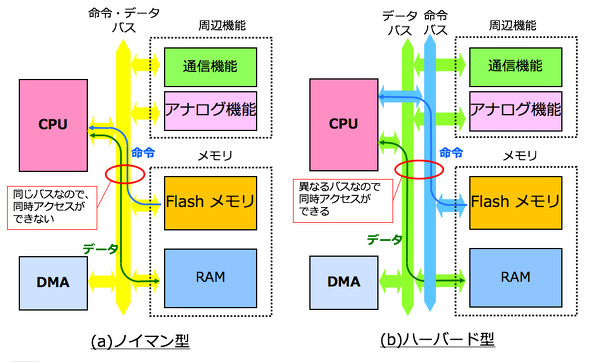
マイコンでは、命令とデータを扱うバスは必須だ。1つのバスを命令とデータで共有すると、同時に命令とデータが共存できないので、命令フェッチの最中は、データを扱えなくなる。このバスの構成を「ノイマン型アーキテクチャ(Von Neumann architecture)」(以下、ノイマン型)と呼ぶ。1つのバスで、命令もデータも取り扱えるので、コスト面でメリットがあるが、パフォーマンスには限界がある。一方、命令バスとデータバスを分けて独立させた方式が、「ハーバードアーキテクチャ(Harvard architecture)」(以下、ハーバード型)で、マイコンのハードが大規模になり、ノイマン型に比べるとコストが上がる。しかし、命令フェッチとデータ処理が完全に独立して行えるので、パフォーマンスは高くなる。
近年、マイコンの製造プロセスが微細化して、ダイ(マイコン・チップ)サイズをあまり気にせずに高機能を実装できるようになったため、最近のマイコンでは、ハーバード型が主流になっている。
しかし、それでも低コストを追求する場合は、ノイマン型が採用される。例えば、ArmのCortex-M3、M4、M7プロセッサでは、パフォーマンス重視のためハーバード型であるが、Cortex-M0、M0+プロセッサでは、コストが重視されているため、ノイマン型が採用されている。(図4参照)
ハーバードアーキテクチャについては、「Q&Aで学ぶマイコン講座(36):ハーバードアーキテクチャって何?」で詳しく解説している。
Copyright © ITmedia, Inc. All Rights Reserved.