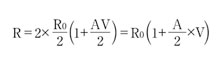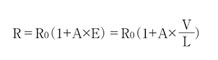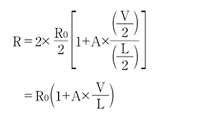次世代アナログLSIでは、素子モデルの標準化が急務（3/4 ページ）

[Shye Shapira/Boris Mishori（Tower Semiconductor），EDN]

抵抗の標準モデル

　上述したように、MOS FETについては標準モデルの策定に進展が見られる。しかし、それによってLSIの設計に必要な標準化が完了するというわけではない。それ以外にも、標準化が必要なのに行われていない事柄はいくつもある。

　抵抗は、いくつかの本質的な機能を表す標準的なモデルが存在しない最も顕著な例である。抵抗のモデル構造はMOS FETのそれよりも簡単に思える。そのため、標準化団体は抵抗のモデル化に高い優先度を設定していない。標準的なシミュレータにはいくつかのモデルが存在するが、多くのファブは基本的な抵抗や寄生容量のセグメントから成るサブ回路を提供している。シミュレータ用のモデルの構成を新たに設計し、シミュレータ間でモデルを変換する場合は、それらが同一の機能を表現し、領域の割り当てや寄生ダイオードの極性に誤りが生じないように注意しなければならない。これは実は面倒な作業である。より複雑なMOS FETモデルですら、モデルパラメータを抽出してシミュレータに組み込めば、多少結果に違いはあるものの、異なるシミュレータにおいても同等に動作するのに、抵抗ではそのようにはいかない。

　通常、PDK（process design kit）のモデルの使い方はMOSモデルより複雑である。例えば、サブ回路のモデルを使用する際、PDKでは特別なインスタンス名を指定しなければならない。シミュレータによってはセグメント化された抵抗サブ回路を使用するために、この指定が必要になる。

　ファウンドリは、電圧/温度の係数を用いて抵抗値の変動を表す基本抵抗モデルを提供している。電圧係数は端子電圧に依存する抵抗の変動を表すが、この係数はファウンドリが特性評価したジオメトリでのみ有効なため、経験の浅い設計者の誤解を招いてしまう恐れがある。　電圧係数を用いたモデル化の限界を示す例として、電圧依存性が以下の式で表される抵抗について考えてみる。

　ここで、Vは抵抗両端の電位差、R0は低電圧でバイアスされている場合の抵抗値、Aは線形の電圧係数である。抵抗の両端の電位差が十分に小さい場合、高次の電圧係数は無視することができる。オームの法則を適用し、1つの抵抗を、それぞれV/2の電圧降下が生じる2つの抵抗を直列に接続したものと考えると、以下の式が成り立つ。

　つまり、抵抗がいくつの部分から成るかに依存して、新しい電圧係数が必要になるということになる。　一方、電界は、拡散抵抗などバルク材料の伝送特性に直接的な影響を与える。電界に依存する抵抗を表すのには、以下の式を使用することができる。

　ここで、Eは電界、Vは電圧、Lは抵抗の長さである。これを用いると、以下の式が成り立つ。

　抵抗を2つの部分に分けて、各部分の電圧と長さがそれぞれ1/2であると見なすと、以下のようになる

　つまり、上記のように見なしても電界は変化しないため、結果として式は変わらないということだ。先述した通り、抵抗の電圧係数をモデル化する場合、そのモデルはファウンドリが特性評価を行ったジオメトリでのみ有効である。

　電圧係数が正の場合、長さが短い素子では電界がより強くなるので、電圧依存性が大きくなる。高い精度を得るために、各ファブは面積の大きい抵抗を使用することを推奨している。また面積の大きい抵抗は、幅などのばらつきを補正する上でも都合が良い。長さが短い素子に関しては、電圧係数を特性データを用いて補完することによりモデルの修正を行う。抵抗の基本モデルでは、基板の電位に対する抵抗の変動分も考慮されない。

　CMCは、最近になって、抵抗モデルを電界ベースのモデルとして標準化する活動を開始した。現在のところ、2端子抵抗モデルを採用しており、温度/電界への依存性、自己発熱、1/fノイズを考慮したものとなっている。CMCは、3端子抵抗、LDMOS（laterally diffused MOS：横方向拡散MOS）など、その他の部品の標準化についても検討中だ。