並走する荷電粒子に働く力：Signal Integrity

[Howard Johnson，EDN]

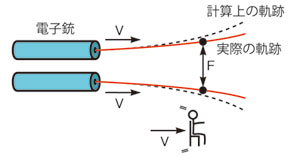
　2個の荷電粒子が、同一の初速度Vで完全な真空中に同時に放出されたとする。それらの粒子が同一の極性（正または負）に帯電している場合には、両粒子間に、反発する力（斥力）が働く。この電気的斥力Fによって、粒子の動きは互いに遠ざかるような軌跡を描く（図1）。

図1　電子銃から放たれた2個の荷電粒子の運動軌跡　相互に働く電気力によって、2個の荷電粒子は徐々に遠ざかっていく。

　軌跡の遠ざかる割合（離隔率）は、各粒子の電気力と質量、初速度が与えられれば、大学レベルの物理学の知識を使うことで計算できる。しかし、その答えはおそらく実際の動きとは異なるものになるだろう。実際の軌跡の離隔率は、電気力（電界効果）のみに基づいた計算結果よりも緩やかなものとなる。物理学者であり数学者でもあるフランス人、 Andre-Marie Ampere氏が存命であるなら、「この現象は磁気力に起因する」と説明するだろう。Ampere氏の見出した法則（アンペールの法則）によれば、同一の向きに電流が流れる平行な電線の間には、互いに引き合う力（引力）が働く。この法則を、わずか2個の荷電粒子が真空中を並走するケースに単純化して当てはめると、荷電粒子には電気力（斥力）とアンペールの法則による磁気力（引力）の両方が働くことになる。それらの力が互いに一部を相殺することにより、図1に示すような実際の軌跡が得られるのである。

　これで一件落着であろうか。実は、この現象を説明するには、次のレベルに思考を進める必要がある。

　図1のように、左から右に移動する2個の荷電粒子の近くを、荷電粒子と同じ速度で並走するいすがあったとしよう。そして、読者がそのいすに座って荷電粒子を観測しているとする。読者から見れば、荷電粒子を放出した電子銃は左後方に遠ざかっていくが、2個の荷電粒子はほぼ静止しているように見える。正確に言えば、読者には荷電粒子が垂直方向にゆっくり遠ざかる動きだけが見えるはずだ。読者から見れば、荷電粒子は水平方向には運動しておらず、磁気力は働いていないことになる。つまり、移動しているいすに座って見れば、荷電粒子は電気的な相互作用のみによって決まる割合で、垂直方向に離れていくということである。

　一方、筆者は地上に置かれた電子銃の傍らに立って観測を行っていたとする。筆者は、磁気力は確かに存在し、粒子の軌跡の広がり方が減速する様子を見ることができる。なぜこのような違いが出るのだろうか。

　このパラドックスを解く鍵は、いすに座っている読者と筆者とでは、時間軸が異なるということだ。読者にとっての時間軸は、その移動速度に依存して、筆者の時間軸よりも少し伸びることになる。筆者の立場から解釈すれば、読者の立場による計算で得られる離隔率は時間軸が伸びるために緩やかになっているということである。

　この実験では、観測者の状況によって磁気力の有無という違いが現われることがわかる。このことから、磁気力は「実体」としての力ではないと言える。言い換えれば、これはアインシュタインの相対性理論から得られる結果そのものなのだ。

　地上に立って観測する筆者の観点から言えば、粒子の運動軌跡は次の3とおりの方法で説明することができる。

• 粒子と同じ速度で運動する観測者の立場から計算する場合は、電界のみが作用するとして計算し、その結果を時間軸の相対的な伸びを考慮して修正する
• 静止した観測者の立場から計算する場合は、アンペールの導入した仮想的な磁気力を実際の値として受け入れ、その作用を含めて計算する
• ただ1つの力として電気力だけが働くとの観点で展開する場合は、電気力の値が粒子と観測者の相対速度に依存して変化するとして説明する

　参考文献1には、3つ目の観点、つまり一元化された電気力学による説明が展開されている。この文献には、相対性理論によってもたらされた成果や一元化された電気力学の意味するところが述べられている。

　以上のように、磁気力が相対論的効果としてもたらされるものだとしても、通常の電気回路において磁界の作用を考慮する必要がないということではない。発電機から高速伝送ラインまで、さまざまな機器や装置を設計する上で、磁気力の観点から検討を行うのは非常に重要なことである。

＜筆者紹介＞

Howard Johnson

Howard Johnson氏はSignal Consultingの学術博士。Oxford大学などで、デジタルエンジニアを対象にしたテクニカルワークショップを頻繁に開催している。ご意見は次のアドレスまで。www.sigcon.comまたは[e-mail]。

脚注

※1…Fukai, Junichiro, A Promenade Along Elec trodynamics, Vales Lake Publishing, 2003